はじめに
このドキュメントは,主に競技プログラミングで出題される問題を解く際に利用できるアルゴリズムやデータ構造をまとめたものです.特定の問題にはあまりフォーカスしないため,問題を解く際の考察の仕方等の内容はありません.詳しく,正確に,分かりやすく書いていこうと思っています.
このドキュメントは執筆途中です.
想定する読者
C++を用いたプログラミングに慣れている方を読者として想定しており,C++言語の仕様や,文法にはあまり触れません.また,計算量という用語についても説明しません.ただし,償却計算量など,計算量の見積もりが複雑なものについては必要に応じて説明します.
コードについて
このドキュメントで登場するコードは,可読性向上のため,以下のようなコードがファイルの先頭に記述してあることを前提としています.また,適切な問題を用いてコードの検証がなされている場合は,コード周辺に
#include <bits/stdc++.h>
#include <atcoder/all>
using namespace std;
using namespace atcoder;
#define i64 int64_t
#define f64 double
const i64 inf = 1e18;
const int dx[] = {0, 1, 0, -1, 1, 1, -1, -1};
const int dy[] = {1, 0, -1, 0, 1, -1, 1, -1};
#define all(a) a.begin(),a.end()
#define overload(_1,_2,_3,_4,name,...) name
#define _rep1(n) for(int i = 0; i < (n); i++)
#define _rep2(i,n) for(int i = 0; i < (n); i++)
#define _rep3(i,a,b) for(int i = (a); i < (b); i++)
#define _rep4(i,a,b,c) for(int i = (a); i < (b); i += (c))
#define rep(...) overload(__VA_ARGS__,_rep4,_rep3,_rep2,_rep1)(__VA_ARGS__)
#define _rrep1(n) for(int i = (n) - 1; i >= 0; i--)
#define _rrep2(i,n) for(int i = (n) - 1; i >= 0; i--)
#define _rrep3(i,a,b) for(int i = (b) - 1; i >= (a); i--)
#define _rrep4(i,a,b,c) for(int i = (b) - 1; i >= (a); i -= (c))
#define rrep(...) overload(__VA_ARGS__,_rrep4,_rrep3,_rrep2,_rrep1)(__VA_ARGS__)
template <class T> bool chmin(T& a, T b){ if(a > b){ a = b; return 1; } return 0; }
template <class T> bool chmax(T& a, T b){ if(a < b){ a = b; return 1; } return 0; }
struct Edge { int to; i64 cost; Edge(int to, i64 cost) : to(to), cost(cost) {} };
using Graph = vector<vector<Edge>>;
フィードバック
もし誤植や,内容に誤りを発見した場合は,是非Twitterなどでフィードバックしていただけると幸いです.
グラフ問題
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph LR
1((1)) --- 2((2))
2((2)) --- 3((3))
2((2)) --- 4((4))
3((3)) --- 1((1))
3((3)) --- 4((4))
4((4)) --- 1((1))
グラフは,ノード(頂点)と,それらを繋ぐエッジ(辺)からなる.このドキュメントでは,特に断りのない限りグラフのノード集合を\(V\),辺集合を\(E\)とする.ノード数は\(|V|\),辺数は\(|E|\)で表される.
グラフでよく出る単語
パス(道)
あるノードから始めて,いくつかの辺をたどって,あるノードにたどり着くまでのノードの列をパス(道)という.有向グラフの場合,向きに従ってたどる必要がある.
また,同じノードを2回通らないパスを単純パスといい,同じ辺を2回通らないパスを路(トレイル)という
閉路
あるノードから始めて,同じノードに戻ってくるパス(始点と終点が同じ路)を閉路という.
次数
あるノードについて,直接繋がっている辺の数を次数という.また,有向グラフでは,入ってくる辺の辺の数を入次数,出ていく辺の数を出次数という.
グラフの種類
無向/有向グラフ
上の図のグラフは辺に向きがなく,無向グラフと呼ばれる.一方で下の図ように辺に向きがあるグラフは有向グラフという.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph LR
1((1)) --> 2((2))
2((2)) --> 3((3))
2((2)) --> 4((4))
3((3)) --> 1((1))
3((3)) --> 4((4))
4((4)) --> 1((1))
重み付きグラフ
下の図のように辺に重みがあるグラフを重み付きグラフという.一般的にノード間の距離や移動コストを表すことが多い.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph LR
1((1)) -- 10 --- 2((2))
2((2)) -- 30 --- 3((3))
2((2)) -- 50 --- 4((4))
3((3)) -- 40 --- 1((1))
3((3)) -- 70 --- 4((4))
4((4)) -- 10 --- 1((1))
連結/非連結グラフ
グラフ上の任意の2ノード間がいくつかの辺をたどって到達可能である(任意の2ノード間にパスが存在する)ものを連結グラフ,そうでない下のようなグラフを非連結グラフという.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph LR
1((1)) --- 2((2))
3((3)) --- 4((4))
単純/多重グラフ
今まで上で出てきたグラフは全て単純グラフである.下のグラフのように,自己ループや多重辺を含むグラフは多重グラフという.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph LR
1((1)) -- 多重辺 --- 2((2))
1((1)) --- 2((2))
2((2)) --- 3((3))
2((2)) --- 4((4))
3((3)) --- 1((1))
3((3)) -- 自己ループ --- 3((3))
3((3)) --- 4((4))
4((4)) --- 1((1))
DAG
閉路を持たない有向グラフを**DAG(有向非巡回グラフ)**という.
プログラムでのグラフの持ち方
プログラム上でのグラフの持ち方は主に2つある.例えば,このような単純連結重み付きグラフの情報を持つ場合,下の2つのような持ち方がある.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph LR
1((1)) -- 10 --> 2((2))
2((2)) -- 30 --> 3((3))
2((2)) -- 50 --> 4((4))
3((3)) -- 40 --> 1((1))
3((3)) -- 70 --> 4((4))
4((4)) -- 10 --> 1((1))
- 隣接行列: 任意の2頂点の辺の取得が\(O(1)\)でできるが,空間計算量が\(O(|V|^2)\).
| i/j | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | - | 10 | - | - |
| 2 | - | - | 30 | 50 |
| 3 | 40 | - | - | 70 |
| 4 | 10 | - | - | - |
- 隣接リスト: 空間計算量が\(O(|V|+|E|)\).
| ノード | 接続された辺のリスト |
|---|---|
| 1 | [{to: 2, cost: 10}] |
| 2 | [{to: 3, cost: 30}, {to: 4, cost: 50}] |
| 3 | [{to: 1, cost: 40}, {to: 4, cost: 70}] |
| 4 | [{to: 1, cost: 10}] |
単一始点最短路(Dijkstra法)
重みが全て\(0\)以上である任意の重み付きグラフ\(G\)における単一始点最短路は,Dijkstra法によって\(O(|E| \log |V|)\)で求めることができる.
単一始点最短路とは,あるノード\(s \in G\)から,\(G\)に含まれる任意のノードまでの最短路である.以降始点を\(s\)と呼ぶ.
説明
以下では,あるノード\(i\)について,\(s\)から\(i\)までの最短路長を\(d_{s→i}\)とする.また,あるノード\(i\)から出てあるノード\(j\)に入る(有向)辺の重みを\(e_{i→j}\)とする.
前提条件から全ての辺の重みが\(0\)以上であるため,\(s\)から到達可能な任意の\(y\)について以下の式が成り立つ.
$$d_{s→y} = min(d_{s→x} + e_{x→y}) \quad ただし \quad d_{s→x} \geq d_{s→y} \quad とする.$$
よって,\(d_{s→y}\)を小さい方から求めていくことで\(s\)を始点とする単一始点最短路を求めることができる.
単一終点最短路
\(G\)に含まれる辺の向きを全て逆向きにしたグラフを\(\hat{G}\)とし,\(i \in G\)に対応する\(\hat{G}\)のノードを\(\hat{i}\)と表す.
任意のノードについて\(s\)を終点とする最短路を求めるには,\(\hat{G}\)について\(\hat{s}\)を始点とした最短路を求めればよい.
説明
以下では,あるノード\(i\)について,\(i\)から\(s\)までの全経路の集合を\(P_{i→s}\)と表す.
任意のノード\(x \in G\)について,\(P_{x→s}\)の辺の向きを全て逆向きにした経路の集合は\(P_{\hat{s}→\hat{x}}\)と明らかに等しいため,\(s\)を終点とする最短路を求めることは\(\hat{s}\)を始点とする最短路を求めることと同義である.
実装
プライオリティキューを用いて,路長優先探索(造語)をすることで求められる.計算量は,取り出しに\(O(\log |V|)\)かかるキューを用いていることから,\(O(|E| \log |V|)\)となる.
コード
pair<vector<i64>, vector<int>> dijkstra(int s, i64 n, Graph &g) {
vector<int> prev(n, -1);
vector<i64> d(n, inf);
d[s] = 0;
priority_queue<pair<i64, int>, vector<pair<i64, int>>, greater<pair<i64, int>>> que;
que.push({0, s});
while (!que.empty()) {
pair<i64, i64> p = que.top();que.pop();
int v = p.second;
if (d[v] < p.first) continue;
for (Edge &e: g[v]) {
if (d[e.to] > d[v] + e.cost) {
d[e.to] = d[v] + e.cost;
prev[e.to] = v;
que.push({d[e.to], e.to});
}
}
}
return {d, prev};
}
// 経路復元
vector<pair<int, int>> get_path(int t, vector<int> &prev) {
vector<pair<int, int>> path;
for (; prev[t] != -1; t = prev[t]) path.push_back({prev[t], t});
reverse(all(path));
return move(path);
}
単一始点最短パス(BFS)
全ての辺の重みが\(1\)の場合の単一始点最短路(単一始点最短パス)は,BFSで\(O(|V|)\)で求められる.
説明
単一始点最短パスをDijkstra法で求めることを考える.Dijkstra法では,始点からの最短路長が小さいノードから順に最短路が求まっていった.全ての辺の重みが\(1\)の場合,最短路長が小さい順というのはすなわち,始点からBFSをした時に訪れる順番であるため,単に始点からBFSをすることで単一始点最短パスを求めることができる.BFSで全てのノードを1回ずつ訪れるので,計算量は\(O(|V|)\).
コード
vector<int> bfs(int node, int n, vector<vector<int>> &g) {
queue<pair<int, int>> q;
vector<bool> visited(n, false);
vector<int> ret(n, -1);
visited[node] = true;
q.push({node, 0});
while (q.size()) {
pair<int, int> v = q.front();
q.pop();
ret[v.first] = v.second;
for (int &e: g[v.first]) {
if (visited[e]) continue;
visited[e] = true;
q.push({e, v.second+1});
}
}
return move(ret);
}
単一始点最短路(Bellman Ford法)
単一始点最短路(SPFA)
全点対最短路(Warshall Floyd法)
全点対最短路(Johnson法)
単一始点最長路
グラフに,始点から到達可能な重みの合計が正の閉路がある場合,その閉路を周ることでいくらでも路長を大きくすることができるため,解は存在しない.
上の条件に当てはまっていない場合,重みの正負を逆転させることで,最短経路問題に変換することができるため,Bellman Ford法(\(O(|V||E|)\))等で解けば良い.自明だが,元のグラフの辺の重みが全て負であった場合は,より高速なDijkstra法(\(O(|E| \log |V|)\))で解くことができる.
また,元のグラフに正の辺があったとしても,グラフが有向非巡回グラフ(DAG)である場合は,ノードをトポロジカルソートをして,順にDPで始点からの最長路求めていく(\(O(|V| + |E|)\))ことができる.
グラフに,始点から到達可能な重みの合計が正の閉路がある場合で,解を求められるように,それぞれのノードは\(1\)回しか通れないというような制約が与えられることがある.これは,巡回セールスマン問題とほぼ同じ問題であるため,NP困難な問題である.bitDPにより\(O(|V|^22^{|V|})\)で解ける.
最小全域木(Kruskal法)
連結性
DFS
Union Find
Low Link
Dynamic Connectivity Algorithm
木
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((1)) --- 2((2))
1 --- 5((5))
2 --- 3((3))
2 --- 4((4))
5 --- 6((6))
5 --- 8((8))
5 --- 9((9))
6 --- 7((7))
グラフのうち,連結でかつ閉路がないグラフを木という. また,その特徴から,次の条件を満たすものは木であると言える.
- 連結で閉路がない
- 閉路がなく\(|E| = |V| - 1\)
- 連結で\(|E| = |V| - 1\)
- 連結で全ての辺が橋
- 閉路がなく,辺を1つ加えると必ず閉路ができる
- 任意の2ノード間のパスが1本
また,任意の連結グラフについて,単一始点最短路を求めたとき,全ノードと,使われた辺の集合で構成されるグラフは木である.(ただし単一始点最短路存在するグラフに限る.)証明は省略する.
木でよく出る単語
根
木では,任意のノードを根と定めることができる.根が定められた木を根付き木という.
深さ
根と定めたノードからの距離を深さという.(ここでいう距離では,辺の重みは考慮しない.) 根付き木において,任意のノードについて,自分と接続された,自分より深さが1低いノードをそのノードの親という.根は親を持たず,根以外のノードは必ず親を1つだけもつ.また,自分と接続された親以外の全てのノードのことを子という.さらに,あるノードから子をたどってたどり着けるノードはそのノードの子孫といい,あるノード\(u\)があるノード\(v\)の子孫であるとき,\(v\)は\(u\)の下にあるという.また,\(u\)を\(v\)の祖先であるという.
部分木
木において,ある1辺を取り除くと,必ず2つの木となる.木から,ある1辺を取り除いて得られる木を全てその木の部分木という.根付き木においてあるノードとその下の部分を取り出した部分とも言える.
また,あるノードからその親
LCA
ある2つのノードが与えられたとき,その2つのノードを自分の下に持つノードを,共通祖先といい共通祖先のうち,最も深さが深い(大きい)ものをその2つのノードの**LCA(最小共通祖先)**という.
n分木
根付き木において,全てのノードが\(n\)個以下の子を持つとき,それをn分木という.また,全てのノードがちょうど\(n\)個の子を持つとき,それを完全n分木という.
DFS
グラフにおいてDFSをすると,橋,関節ノードの列挙や連結成分ごとへのノード集合の分割ができることを上の章で説明した.ここでは,木でDFSするとどのような情報が手に入るかを説明する.
- 木においてあるノードからDFSすると,そのノードからの単一始点距離がわかる.(ここでいう距離は,辺の重みを考慮した距離とみなしてもよい.)
- 根付き木において根からDFSすると,任意のノードの深さ,親がわかる.
他にもいろいろな情報が手に入るのだが,それは後の章で説明する.
直径
2ノード間距離のうち最大のものを,そのグラフの直径という.ここでいう距離は,辺の重みは考慮しない.
木の直径は,2回のDFSで求めることができる.具体的には,任意のノードについて,最も遠いノードを求め,そのノードからまた最も遠いノードを求めると,後者の距離が木の直径である.以下に証明を示す.
証明
任意に選択したノード\(r\)から最も遠いノード\(x\)は直径の端点にならないと仮定する.直径(複数ありうる)の端点の集合を\(\mathbb{E}\)とする.\(r\)->\(x\)パスが直径と最初に交わる点が存在すればそれを\(h\)とする.
- \(h\)が存在する時
\(r\)->\(h\)->\(x\)となるパスが存在する.この時,\(h\)は直径上にあるので,\(h\)から最も遠いノードは\(\mathbb{E}\)に属するノードである.ここで,\(r\)から最も遠いノードは\(x\)なので\(x\)は\(\mathbb{E}\)に属する.これは\(x\)が直径の端点にならないことに⽭盾する.
- \(h\)が存在しない時
以下の式から,\(x\)を端点とする直径を構成することができるため,\(x\)が直径の端点にならないことに⽭盾する.
\(dist(r, x) \geq dist(r, h) + max_{u \in \mathbb{E}}(dist(h, u))\)
よって\(dist(h, x) \geq + max_{u \in \mathbb{E}}(dist(h, u))\)
以上から,背理法より,任意に選択したノード\(r\)から最も遠いノード\(x\)は直径の端点になる.したがって,任意のノードについて,最も遠いノードを求め,そのノードのから最も遠いノードまでの距離が直径となる.
コード
pair<int, int> dfs(int node, int parent, vector<vector<int>> &g) {
pair<int, int> ret = {0, node};
for (int &e: g[node]) {
if (e == parent) continue;
pair<int, int> tmp = dfs(e, node, g);
tmp.first++;
chmax(ret, tmp);
}
return move(ret);
}
int diameter(vector<vector<int>> &g) {
pair<int, int> d = dfs(0, -1, g);
d = dfs(d.second, -1, g);
return d.first;
}
Euler Tour
Euler Tour Tree
HL分解
2項演算(以降便宜上仮に"和"と呼ぶ)を与える. HL分解の各操作と時間計算量は以下.
- 構築: \(O(|V|)\)
- 木のLCA: \(O(\log |V|)\)
- 木の任意のノードの値(モノイド)の更新: \(O(\log |V|)\)
- 木の任意2ノード間のパスクエリ: \(O(\log ^2|V|)\)
※パスクエリというのは,あるパスについて,通った順番にノード上の値を累積"和"した値を求めるクエリのこと.
説明
はじめに,以下のように枝分かれのない極端な木を考える.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph LR
1((1)) --- 2((2)) --- 3((3)) --- 4((4)) --- 5((5))
木に枝分かれがない場合(全てのノードの次数が2以下の木の場合),これは単純にノードの一次元配列と見なすことができる.よって,このような木であれば,値の更新,および任意のパスにおけるパスクエリに高速に答えるためにはセグメント木を用いればよいことがわかる.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((1)):::heavy --- 2((2)):::heavy
1 --- 9((9)):::heavy
1 --- 5((5)):::heavy
2 --- 3((3)):::heavy
2 --- 4((4)):::heavy
5 --- 6((6)):::heavy
5 --- 8((8)):::heavy
6 --- 7((7)):::heavy
9 --- 10((10)):::heavy
linkStyle 2 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 4 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 5 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 7 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 8 stroke-width:4px,fill:none,stroke:slateblue;
classDef heavy stroke-width:4px,stroke:slateblue;
では任意の木においてこれらのクエリに答えるためには,木をいくつかのパスに分解し,分割した各パスにおいては累積"和"を求めるためにセグメント木を利用し,それらを合わせればいいのではないか.これがHL分解の基本的なアイディアである.
例えば上のように木をいくつかのパスに分解すると,1->7パスや6->1パスのように,パス上の全てのノードが同じセグ木上で連続した並びになっているパスは1回のセグ木に対する操作でパスクエリが求まり,6->10パスのようなパスでは6->1と9->10で合わせて2回セグ木で操作を行い,それらを合わせればよいということである.
しかし,異なるセグ木を操作した回数を\(N\)とすると,パスクエリに対する計算量は当然\(O(N \log |V|)\)となるため,各セグ木の操作が高速でも,この\(N\)が大きくなるとパスクエリに高速に答えることができない.
ここからは,この\(O(N)\)を小さくするためのアイディアについて説明する.
結論からいうと,各親から見て,部分木のノード数が最も多い子への辺を選択する.(個数が同じ子が複数ある場合はどれを選んでも良い.)選択した辺をheavy辺といい,選択しなかった辺をlight辺という.(HL分解はHeavy-Light分解を意味している.)
つまり,任意のパスにおいて,連続したheavy辺(以下heavyパスと呼ぶ)の個数が先ほどの\(N\)となる.任意のパス上でheavyパスの個数が最大いくつになるかを考えると少し難しいので,まずはパスの終点を木の根と仮定して考える.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((1)) --- 2((2))
1 --- 6((6))
2 --- 3((3))
3 --- 4((4))
3 --- 5((5))
6 --- 7((7))
7 --- 8((8))
8 --- 9((9))
8 --- 10((10))
6 --- 11((11))
1 --- 12((12))
12 --- 13((13))
13 --- 14((14))
13 --- 15((15))
13 --- 18((18))
15 --- 16((16))
15 --- 17((17))
18 --- 19((19))
まずはheavy辺とlight辺に塗り分ける.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((1)):::heavy --- 2((2)):::heavy
1 --- 6((6)):::heavy
1 --- 12((12)):::heavy
2 --- 3((3)):::heavy
3 --- 4((4)):::heavy
3 --- 5((5)):::heavy
6 --- 7((7)):::heavy
6 --- 11((11)):::heavy
7 --- 8((8)):::heavy
8 --- 9((9)):::heavy
8 --- 10((10)):::heavy
12 --- 13((13)):::heavy
13 --- 14((14)):::heavy
13 --- 15((15)):::heavy
13 --- 18((18)):::heavy
15 --- 16((16)):::heavy
15 --- 17((17)):::heavy
18 --- 19((19)):::heavy
linkStyle 2 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 3 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 4 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 6 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 8 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 9 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 11 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 13 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 15 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 17 stroke-width:4px,fill:none,stroke:slateblue;
classDef heavy stroke-width:4px,stroke:slateblue;
この木を例にしながら,任意の点から根までのパスにいくつのheavyパスが含まれるかを考える.ノード1個単体で,どこにもheavy辺が伸びていないものも1つのheavyパスとみなすと,任意のパスにおいて,heavyパスと1本のlight辺を交互に通ることになる.そのため,パス上のheavyパスの個数とパス上のlight辺の個数の差は必ず\(1\)以下になる.つまり,パス上のheavyパスの個数を抑えることは,パス上のlight辺の個数を抑えることと言い換えることができる.
仮に,始点をノード19,終点を根としよう.まず,19->18の累積"和"を対応するセグ木を使って求める.次の18->13を見ると,これはlight辺である.ここにlight辺があるということはつまり,ノード18を根とする部分木のサイズ(ノード数)は,最大でも,ノード13を根とする部分木のサイズの半分以下ということである.もし半分以上のサイズならここはheavy辺になっているはずだからだ.実際に,ノード13を根とする部分木のサイズは7,ノード18を根とする部分木のサイズは2であり,半分以下である.これはつまり,light辺を通るたびに,全体の推定ノード数が,その下の部分木のサイズの2倍(以上)になるということである.したがって,全体のノード数を\(|V|\)とすると,任意のノードから根までのパスに,light辺は最大でも\(O(\log |V|)\)個しか含まれないことがわかる.従って,heavyパスの個数のオーダも\(O(\log |V|)\)であり,また,それぞれのheavyパスにおいて,セグ木の操作により\(O(\log |V|)\)がかかるため,任意のノードから根までのパスクエリの計算量は\(O(\log ^2 |V|)\)である.
最後に,任意の2ノード間\(u\)->\(v\)のパスクエリを求める計算量は,\(u\)->\(root\) \(+\) \(root\)->\(v\)のパスクエリの計算量より小さいことに注目すると,後者の計算量は\(O(2 \log ^2 |V|) = O(\log ^2 |V|)\)であるため,前者の計算量も\(O(\log ^2 |V|)\)で抑えられることがわかる.
LCAを求めるクエリについても,上と同様にlight辺の個数は\(O(\log |V|)\)であるため,高々\(O(\log |V|)\)回上るとLCAにたどりつけることがわかる.
実装
先ほどの木を例として考える.
パスクエリ
まずはパスクエリから.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((1)):::heavy --- 2((2)):::heavy
1 --- 6((6)):::heavy
1 --- 12((12)):::heavy
2 --- 3((3)):::heavy
3 --- 4((4)):::heavy
3 --- 5((5)):::heavy
6 --- 7((7)):::heavy
6 --- 11((11)):::heavy
7 --- 8((8)):::heavy
8 --- 9((9)):::heavy
8 --- 10((10)):::heavy
12 --- 13((13)):::heavy
13 --- 14((14)):::heavy
13 --- 15((15)):::heavy
13 --- 18((18)):::heavy
15 --- 16((16)):::heavy
15 --- 17((17)):::heavy
18 --- 19((19)):::heavy
linkStyle 2 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 3 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 4 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 6 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 8 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 9 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 11 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 13 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 15 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 17 stroke-width:4px,fill:none,stroke:slateblue;
classDef heavy stroke-width:4px,stroke:slateblue;
17->19のパスクエリを求めてみる.
- ノード17を左ノード,ノード19を右ノードとする.
- ノード17が含まれるheavyパスで最も根に近いノード(以降topノードと呼ぶ)と,ノード19のtopノードの深さを比較する.ノード17とノード18では,ノード17の方が深いため,ノード17の値を左側から累積した後,左ノードをノード15に移動する.
- ノード15のtopノードと,ノード19のtopノードの深さを比較すると,今度はノード1よりもノード18の方が深いため,19->18を右側から累積した後,右ノードをノード13に移動する.
- ノード15のtopノードとノード13のtopノードが等しいことから,これらは同じheavyパス上にあることがわかる.よって,単に左ノード->右ノードで値を累積し,左側の累積値に累積する.
- 最後に左側の累積値と右側の累積値の"和"を取った値が求める値である.
このようにしてパスクエリを求めることができる.ここで,パスクエリを求める疑似コードを示す.
fn query(lnode, rnode) -> S {
let prodl: S = e() // 左側の累積値を単位元で初期化
let prodr: S = e() // 右側の累積値を単位元で初期化
while true {
if lnode.top == rnode.top { // 左ノードと右ノードが同じheavyパスにある場合
if lnode.depth > rnode.depth
prodl = op(prodl, prod(lnode, rnode)) // 左ノード->右ノードパスの累積値を左側に累積
else
prodr = op(prod(rnode, lnode), prodr) // 右ノード->左ノードパスの累積値を右側に累積
return op(prodl, prodr) // 左側の累積値と右側の累積値の"和"を返す
}
// topノードの深さの深い方を上にあげる
if lnode.top.depth > rnode.top.depth { // 左ノードのtopノードの方が深さが深い場合
prodl = op(prodl, prod(lnode, lnode.top)) // 左ノード->topパスの累積値を左側に累積
lnode = lnode.top.parent // lnodeを上にあげる
} else { // 右ノードのtopノードの方が深さが深い場合
prodr = op(prod(rnode.top, rnode), prodr) // top->右ノードパスの累積値を右側に累積
rnode = rnode.top.parent // rnodeを上にあげる
}
}
}
構築
上の疑似コードから,パスクエリを求めるにはそれぞれのノードのtopノード,深さ,親,heavyパス上での位置などの情報が必要となることがわかる.これらを,最初に構築フェースで求める.これらは,木を2回DFSすることで全て求めることができる.
まず,それぞれのノードの木上での深さ,親は,1回DFSをすることで求められる.また,その際に,下の部分木のサイズを足しながら親に戻っていくことで,各親はheavy辺を決定することができる.2回目のDFSでは,heavy辺を優先したDFSを行うことでtopノードを求めることができる.また,その際,通ったノードを順に並べていくことで,各heavyパス上での位置も求めることができる.
2回目のDFSの説明が分かりづらいと思うので,先ほどの木を例に説明する.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((1)):::heavy --- 2((2)):::heavy
1 --- 6((6)):::heavy
1 --- 12((12)):::heavy
2 --- 3((3)):::heavy
3 --- 4((4)):::heavy
3 --- 5((5)):::heavy
6 --- 7((7)):::heavy
6 --- 11((11)):::heavy
7 --- 8((8)):::heavy
8 --- 9((9)):::heavy
8 --- 10((10)):::heavy
12 --- 13((13)):::heavy
13 --- 14((14)):::heavy
13 --- 15((15)):::heavy
13 --- 18((18)):::heavy
15 --- 16((16)):::heavy
15 --- 17((17)):::heavy
18 --- 19((19)):::heavy
linkStyle 2 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 3 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 4 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 6 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 8 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 9 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 11 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 13 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 15 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 17 stroke-width:4px,fill:none,stroke:slateblue;
classDef heavy stroke-width:4px,stroke:slateblue;
この木でheavy辺を優先したDFSを行い,通ったノードを順に並べるとこのようになる.
|1|12|13|15|16|17|14|18|19|2|3|4|5|6|7|8|9|10|11|
すると,heavy辺を優先して探索したため,全てのheavyパスが,この配列の連続する部分列として現れていることがわかる. これを1本のセグ木に持ち,各ノードのインデックスを持っておくことで,1本のセグ木だけで任意のheavyパスの累積値を求めることができる.
この構築フェーズは,木上でDFSを2回行うだけなので,計算量は\(O(|V|)\)である.
実装におけるその他の注意事項
実装上注意すべきことをいくつか最後に述べる.
まず1つ目は,パスクエリでは,向きを間違えてはいけないということ.このページでは"和"と呼んでいるが,実際にはこの2項演算には可換性を要求しないので,可換ではない可能性があることを忘れてはいけない.\(u\)->\(v\)の累積値を求めるなら,最左を\(u\),最右を\(v\)として,累積値を取るときに右側からとるのか左側から取るのかを間違えてはいけない.
2つ目は,先ほどセグ木は1本と言ったが実際には2本必要であるということ.任意のheavyパスは,パスによっては右からも左からも累積値を取る可能性がある.よって,2方向分で2本セグ木が必要である.パスクエリの実装の際に,どっちのセグ木を使うかを間違えないように注意する.
以上!
コード
class Node {
public:
int depth, parent, top, idxf, idxb;
Node() : parent(-1) {}
};
template <class S, S (*op)(S, S), S (*e)()> class HLD {
public:
HLD() : HLD(vector<vector<int>>(0), -1) {}
explicit HLD(vector<vector<int>> &tree, int root_)
: HLD(tree, root_, vector<S>(int(tree.size()), e())) {}
explicit HLD(vector<vector<int>> &tree, int root_, const vector<S> &v)
: n(int(tree.size())), root(root_) {
build_(tree, v);
}
void build(vector<vector<int>> &tree, int root_) {
n = int(tree.size());
build(tree, root_, vector<S>(n, e()));
}
void build(vector<vector<int>> &tree, int root_, const vector<S> &v) {
n = int(tree.size());
root = root_;
build_(tree, v);
}
// set element to node
void set(int node, S x) {
stf.set(nodes[node].idxf, x);
stb.set(nodes[node].idxb, x);
}
// lca
int lca(int ln, int rn) {
while (1) {
int topl = nodes[ln].top, topr = nodes[rn].top;
if (topl == topr) {
if (nodes[ln].depth < nodes[rn].depth) return ln;
else return rn;
}
if (nodes[topl].depth > nodes[topr].depth) ln = nodes[topl].parent;
else rn = nodes[topr].parent;
}
}
// path query
S query(int ln, int rn) {
S prodl = e(), prodr = e();
while (1) {
int topl = nodes[ln].top, topr = nodes[rn].top;
if (topl == topr) {
if (nodes[ln].depth < nodes[rn].depth) { // rn is deeper than ln
prodl = op(prodl, stf.prod(nodes[ln].idxf, nodes[rn].idxf+1));
} else { // ln is deeper than rn
prodl = op(prodl, stb.prod(nodes[ln].idxb, nodes[rn].idxb+1));
}
return op(prodl, prodr);
}
if (nodes[topl].depth > nodes[topr].depth) {
prodl = op(prodl, stb.prod(nodes[ln].idxb, nodes[topl].idxb+1));
ln = nodes[topl].parent;
} else {
prodr = op(stf.prod(nodes[topr].idxf, nodes[rn].idxf+1), prodr);
rn = nodes[topr].parent;
}
}
}
private:
int n, root;
segtree<S, op, e> stf, stb;
vector<Node> nodes;
void build_(vector<vector<int>> &tree, const vector<S> &v) {
assert(n == int(v.size())); assert(root < n);
// create segtree
stf = segtree<S, op, e>(n);
stb = segtree<S, op, e>(n);
nodes = vector<Node>(n);
vector<int> heavy(n, -1);
pp1(tree, heavy, root, root, 0);
pp2(tree, v, heavy, 0, root, root, root);
}
// set heavy node, parent, depth
int pp1(vector<vector<int>> &tree, vector<int> &heavy, int node, int p, int d) {
nodes[node].parent = p;
nodes[node].depth = d;
int sz = 1, sz_max = 0, sz_c;
for (int &c: tree[node]) {
if (c == p) continue;
sz_c = pp1(tree, heavy, c, node, d+1); // get child's size
sz += sz_c; // update size
if (chmax(sz_max, sz_c)) heavy[node] = c; // update heavy node
}
return sz;
}
// build segtree, set top
int pp2(vector<vector<int>> &tree, const vector<S> &v, vector<int> &heavy, int tour_idx, int node, int p, int t) {
nodes[node].idxf = tour_idx;
stf.set(tour_idx++, v[node]);
nodes[node].idxb = n - tour_idx;
stb.set(n - tour_idx, v[node]);
nodes[node].top = t; // set top
if (heavy[node] >= 0) { // heavy node and depth first search
tour_idx = pp2(tree, v, heavy, tour_idx, heavy[node], node, t);
}
for (int &c: tree[node]) {
if (c == p || c == heavy[node]) continue;
tour_idx = pp2(tree, v, heavy, tour_idx, c, node, c); // next node is top
}
return tour_idx;
}
};
Link Cut Tree
巡回セールスマン問題
\(N\)個のノード\(1, 2, ..., N\)を持つ重み付き有向グラフ\(G(V, E)\)について,ノード\(1\)から出発し,各ノードをちょうど1度ずつ通りノード\(1\)へ戻る閉路の中で最短の経路の距離を求めよ.
この問題はNP困難というクラスに属する有名な問題で,多項式時間で解くアルゴリズムが存在しないとされている.bitDPというアルゴリズムを使うと,\(O(|V|^22^{|V|})\)で解くことができる.
具体的には以下の漸化式が成立する.
$$ dp[\mathbb{S}][v] = min_{u \in (\mathbb{S}\backslash \lbrace v \rbrace)}(dp[S\backslash \lbrace v \rbrace][u] + dist[u][v]) $$
自然言語でいうなら,「今まで訪れたノードの集合が\(\mathbb{S}\)で最後に訪れたノードが\(v\)になるような最短経路は,今までノードの集合が\(\mathbb{S}\backslash \lbrace v \rbrace\)で最後に訪れたノードが\(\mathbb{S}\backslash \lbrace v \rbrace\)に含まれるいずれかのノードであるような最短経路にそのノードから\(v\)への距離を足した値の最小値」.
この訪れたノードの集合をbitで持つ.この集合の状態数は\(2^|V|\)となり,最後に訪れたノードの状態数は\(|V|\)である.各状態から,次に通る都市を\(|V|\)通り探索するので,全体の計算量は\(O(|V|^22^{|V|})\)となる.
コード
i64 tsp(int n, vector<vector<int>> &dist) {
vector<vector<i64>> dp(1<<n, vector(n, inf));
dp[0][0] = 0;
rep (bit, 1<<n) {
rep (u, n) {
if (!((bit >> u)&1) and bit + u != 0) continue;
rep (v, n) {
if ((bit >> v)&1) continue;
chmin(dp[bit|(1<<v)][v], dp[bit][u] + dist[u][v]);
}
}
}
return dp[(1<<n)-1][0];
}
区間問題
配列や座標におけるある区間や範囲に対して,何らかの操作を高速に行う必要があるときがある.区間に対する操作では,1度に多くのデータを扱うことが多いため,適切なデータ構造を用いる必要があることが多い.
imos法
配列の長さを\(N\)とする.imos法により,区間更新を複数回行った後の,配列の各要素の値を得ることができる.操作の時間計算量は以下.
- 区間更新: \(O(1)\)
- 配列の各要素の値の取得\(O(N)\)
配列の各要素は群を成す集合の要素である必要がある.
説明
群における2項演算を仮に和として考える.
imos法でいう区間更新とは,配列のある区間の全要素に同じ値を足す操作のことである.これは,愚直に行うと\(O(N)\)かかってしまう.
imos法は,どの区間に何の値を足す必要があるかという情報を覚えておき,配列の要素を最後に取得する時に,それまでの区間更新をまとめて処理するという方法である.より具体的に説明すると,区間更新操作では,左から累積和(\(O(N)\))を取った時に,配列の各要素の値を得られるように値の更新を行う.
最後に左から累積和を取ることを前提として考えると,配列のある要素にある値を足すことは,その要素以降の全要素にその値を足すことを意味する.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| クエリ1 | - | \(+1\) | \(+1\) | \(+1\) | \(+1\) | \(+1\) | \(+1\) | \(+1\) |
| 更新1 | \(0\) | \(+1\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) |
| 累積和 | \(0\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) | \(1\) |
よって,例えばある区間に値\(x\)を足す場合,区間クエリの先頭に\(x\)を足し,終わりに\(-x\)を足すことで,最後に累積和を取った時にその区間の要素のみに\(x\)を足すことができる.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| クエリ1 | - | \(+x\) | \(+x\) | \(+x\) | \(+x\) | - | - | - |
| 更新1 | \(0\) | \(+x\) | \(0\) | \(0\) | \(0\) | \(-x\) | \(0\) | \(0\) |
| 累積和 | \(0\) | \(x\) | \(x\) | \(x\) | \(x\) | \(0\) | \(0\) | \(0\) |
区間更新が複数あっても操作は変わらない.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| クエリ1 | - | \(+x\) | \(+x\) | \(+x\) | \(+x\) | - | - | - |
| 更新1 | \(0\) | \(+x\) | \(0\) | \(0\) | \(0\) | \(-x\) | \(0\) | \(0\) |
| クエリ2 | - | - | \(+y\) | \(+y\) | \(+y\) | \(+y\) | - | - |
| 更新2 | \(0\) | \(+x\) | \(+y\) | \(0\) | \(0\) | \(-x\) | \(-y\) | \(0\) |
| クエリ3 | - | - | - | \(+z\) | \(+z\) | - | - | - |
| 更新3 | \(0\) | \(+x\) | \(+y\) | \(+z\) | \(0\) | \(-x-z\) | \(-y\) | \(0\) |
| 累積和 | \(0\) | \(x\) | \(x+y\) | \(x+y+z\) | \(x+y+z\) | \(y\) | \(0\) | \(0\) |
扱う代数系を群一般としてまとめると,区間\([l, r))に値\(x\)を作用させる場合,配列の\(l\)番目に\(x\)を作用させ,\(r\)番目に\(x\)の逆元を作用させる.実際の値を得るには,左から累積値を取れば良い.
コード
template <class S, S (*op)(S, S), S (*e)(), S (*inv)(S)> struct Imos {
private:
vector<S> v;
public:
Imos(int size) { v.assign(size, e()); }
void query(int l, int r, S x) { // [l, r)
v[l] = op(v[l], x);
v[r] = op(v[r], inv(x));
}
vector<S> get_values() {
rep (i, 1, v.size()) v[i] = op(v[i-1], v[i]);
return move(v);
}
};
セグメント木
区間クエリを求めたい配列の長さを\(N\)とすると,セグメント木の各操作と時間計算量は以下.
- 構築: \(O(N)\)
- 値(モノイドを成す集合の要素)の更新: \(O(\log N)\)
- 配列の任意の区間の"和"(モノイドにおける2項演算): \(O(\log N)\)
説明
配列の区間の累積"和"を木で管理することで,区間クエリ,更新クエリを高速に計算する.
配列の初期値を
|50|10|70|30|10|90|40|
として,配列の要素を葉とする2分木を構築すると,このようになる.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1(( )) --- 2(( ))
1 --- 3(( ))
2 --- 4(( ))
2 --- 5(( ))
3 --- 6(( ))
3 ---- 7((40))
4 --- 8((50))
4 --- 9((10))
5 --- 10((70))
5 --- 11((30))
6 --- 12((10))
6 --- 13((90))
ノードを集約する上のノードに,子の"和"を持たせるとこのようになる.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((300)) --- 2((160))
1 --- 3((140))
2 --- 4((60))
2 --- 5((100))
3 --- 6((100))
3 ---- 7((40))
4 --- 8((50))
4 --- 9((10))
5 --- 10((70))
5 --- 11((30))
6 --- 12((10))
6 --- 13((90))
先に更新クエリを考える.例えば配列の左から3番目の値70を20に更新するとこのようになる.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((250)):::heavy --- 2((110)):::heavy
1 --- 3((140))
2 --- 4((60))
2 --- 5((50)):::heavy
3 --- 6((100))
3 ---- 7((40))
4 --- 8((50))
4 --- 9((10))
5 --- 10((20)):::heavy
5 --- 11((30))
6 --- 12((10))
6 --- 13((90))
linkStyle 0 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 3 stroke-width:4px,fill:none,stroke:slateblue;
linkStyle 8 stroke-width:4px,fill:none,stroke:slateblue;
classDef heavy stroke-width:4px,stroke:slateblue;
更新する場所を青く示している.どの場所を更新しても,木の高さ個のノードしか変化せず,かつ,この木は偏りのない2分木であるため,更新クエリは\(O(\log N)\)である.
次に区間クエリを考える.これは,左側の累積"和"と右側の累積"和"に分けて考えるとわかりやすい.
例として配列の2番目から6番目までの累積"和"を求める.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((250)) --- 2((110))
1 --- 3((140))
2 --- 4((60))
2 --- 5((50)):::heavy1
3 --- 6((100)):::heavy2
3 ---- 7((40))
4 --- 8((50))
4 --- 9((10)):::heavy1
5 --- 10((20))
5 --- 11((30))
6 --- 12((10))
6 --- 13((90))
classDef heavy1 stroke-width:4px,stroke:green;
classDef heavy2 stroke-width:4px,stroke:orangered;
緑が左側の累積"和"で使う値,赤が右側の累積"和"で使う値を示している.どのような区間クエリであってっも,左側と右側それぞれには,同じ深さのノードは1度しか現れない.なぜなら,同じ深さのノード2つは上のノード1つで集約できるはずだからである.
よって,区間クエリの計算量も\(O(\log N)\)である.
実装
区間クエリを求めたい配列の要素数が変化しないと仮定すると,セグメント木の構造は静的であり変化しないことがわかる.これを利用して,セグ木の実装ではノードを単に\(2*N-1\)この配列で管理することができる.
ノードを管理する配列上でのそのノードのインデックスを示すと,このようになる.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((1)) --- 2((2))
1 --- 3((3))
2 --- 4((4))
2 --- 5((5))
3 --- 6((6))
3 ---- 7((13))
4 --- 8((7))
4 --- 9((8))
5 --- 10((9))
5 --- 11((10))
6 --- 12((11))
6 --- 13((12))
しかし,これではこのように構築すると,親<->子間のインデックスに規則性がなく,非常に扱いづらくなる.
そこで,以下のような工夫が考えられる.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((1)) --- 2((2))
1 --- 3((3))
2 --- 4((4))
2 --- 5((5))
3 --- 6((6))
3 ---- 7((7))
4 --- 8((8))
4 --- 9((9))
5 --- 10((10))
5 --- 11((11))
6 --- 12((12))
6 --- 13((13))
先ほどと比較して何が嬉しいかというと,この木では,親のインデックスを\(i\)とすると子のインデックスは必ず\(\lbrace 2 \times i, 2 \times i+1 \rbrace\)になっており,さらに,子のインデックスを\(i\)とすると,その親のインデックスは必ず\(i/2\)になっている.
そのため,このように構築することで親<->子間の移動が非常に楽になり,実装が短くなる.
しかし,気づいている方もいるかもしれないが,この実装だと,親の累積"和"において子の順序が保たれていないため,任意のモノイドをのせることはできない.
しかし,モノイドではなく,和や積,min,maxというような可換性を有する2項演算はのせることができるため,その場合は問題ない.例えば,後の章で扱うが,2次元区間クエリを扱うような場合,可換性を有さないモノイドをのせることはあまりないと考えられるため,ノード数を少なく抑えられるこの実装は有用である.
では,任意のモノイドをのせるためにはどうすればいいかというと,下のように構築すると良い.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
1((1)) --- 2((2))
1 --- 3((3))
2 --- 4((4))
2 --- 5((5))
3 --- 6((6))
3 --- 7((7))
4 --- 8((8))
4 --- 9((9))
5 --- 10((10))
5 --- 11((11))
6 --- 12((12))
6 --- 13((13))
7 --- 14((14))
7 --- 15((15))
先ほどよりノード数が多くなっている.これは,要素数を超える最小の2の冪乗の値を要素数にするという実装である.余分に枠を取ることで,子の順序を保ったまま親に累積"和"を持たせることができる.また,先ほどと同様に親<->子間の移動も楽である.
ノード数は最大でも\(2\)倍程度しか増えないため,空間計算量も時間計算量も変化しない.
コード
Binary Indexed Tree(フェニック木)
2項演算(以降便宜上仮に"和"と呼ぶ)を与える. 区間クエリを求めたい配列の長さを\(n\)とすると,**Binary Indexed Tree(BIT)**の各操作と時間計算量は以下.
- 値(モノイド)の更新: \(O(\log N)\)
- 配列の始めから任意のインデックスまでの累積"和": \(O(\log N)\)
説明
配列に単に値を持った場合,値の更新が\(O(1)\)でできる代わりに任意のインデックスまでの累積"和"を求めるのには\(O(N)\)かかる.逆に配列にそのインデックスまでの累積"和"を持つと,累積"和"の取得が\(O(1)\)でできる代わりに値の更新が\(O(N)\)かかってしまう.工夫すると,実はどちらのクエリにも高速(\(O(\log N)\))に答えることができる.
\(O(\log N)\)でこれらの操作をするために,偏りのない2分木を作り,親のノードにその部分木が持つ葉の"和"を持たせるというのが,セグメント木のアイディアであった.
BITでは,数のビット表現に注目する.BITの基本的なアイディアは,任意の自然数がいくつかの2の累乗の和であるのと同様に,累積"和"はいくつかの「サブ累積"和"」の"和"として表すことができるということである.例えばある数をビットで表した時に2つの位置のビットが立っているということは2つの累積"和"を含んでいるということ.
長さ\(16\)の配列にいくつか値を設置した例を見てみる.
| Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 保持する区間 | 1 | 1...2 | 3 | 1...4 | 5 | 5...6 | 7 | 1...8 | 9 | 9...10 | 11 | 9...12 | 13 | 13...14 | 15 | 1...16 |
| 設置した値 | 2 | 0 | 1 | 1 | 1 | 0 | 4 | 4 | 0 | 1 | 0 | 1 | 2 | 3 | 0 | 0 |
| 実際の累積"和" | 2 | 2 | 3 | 4 | 5 | 5 | 9 | 13 | 13 | 14 | 14 | 15 | 17 | 20 | 20 | 20 |
| 格納する値 | 2 | 2 | 1 | 4 | 1 | 1 | 4 | 13 | 0 | 1 | 0 | 2 | 2 | 5 | 0 | 20 |
実際に,BITで累積"和"を求めるにはどうするかというのを説明する.例えば閉区間\([0, 13]\)の累積"和"を求めてみる.まず\(13\)を2進数で表す.
$$13_{(10)} = 1101_{(2)}$$
このインデックスに格納された値を足しては最も右にある\(1\)を削除してそれを新しいインデックスとするという操作を,インデックス値が\(0\)になるまで繰り返す.
$$1101_{(2)} → 1100_{(2)} → 1000_{(2)} → 0000_{(2)}$$
この例ではインデックス\(1101_{(2)} = 13_{(10)}\)の値,インデックス\(1100_{(2)} = 12_{(10)}\)の値,インデックス\(1000_{(2)} = 8_{(10)}\)の値を足せばいいことになる.上の表で実際に足してみると,\(2 + 2 + 13 = 17\)となる.これは,閉区間\([0, 13]\)の実際の累積"和"の値と一致している.また,\(13, 12, 8\)が保持する区間を見てみると,\(1...8, 9...12, 13\)となっていることからも正しい「サブ累積"和"」を足せていることがわかる.
表だとわかりにくいが,これを木構造として見てみるとわかりやすい.
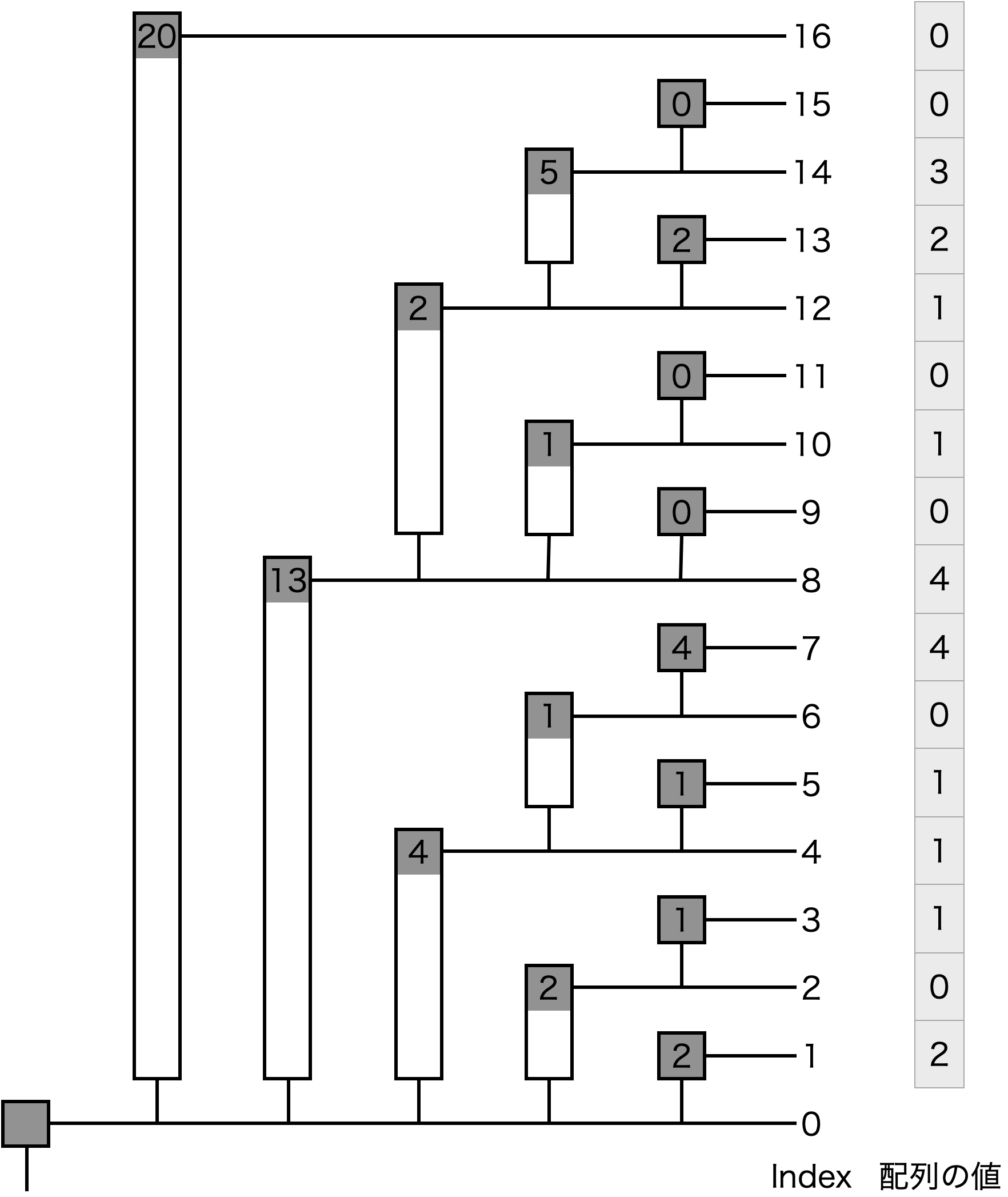
このようにして,ビットが\(1\)になっているところの個数回の演算で,指定されたインデックスまでの累積"和"を求めることが可能であるため,累積"和"を求めるクエリの計算量は,ビット長から,明らかに\(O(\log N)\)である.
最後に値の更新だが,あるインデックスを,自身が保持する区間に含めるインデックスの個数も,ビット長から,明らかに\(O(\log N)\)しかないため,これらのインデックスのみを更新する計算量も,\(O(\log N)\)である.
任意区間の累積"和"を求めたい場合
BITで任意区間の累積"和"が求められるケースは限られている.例えば,整数での和を扱っている場合,閉区間\([a, b]\)の累積和(これは文字通り和)は\([0, b]\)の値から\([0, a-1]\)の値を引くことで求められる.このように,扱っている代数系に,逆元が定義できる場合,つまり,扱っている代数系が群である場合は,BITで任意区間の累積"和"が求めることができる.
実装
説明はややこしく見えるが,コード上では,ビット演算によりアクセスすべきインデックスを簡単に計算できるため,実装は軽い.例えば,ある数\(x\)を2進数表した時に最も右にある\(1\)だけを取り出すには,\(x&(-x)\)とするだけである.
Fenwickさんの論文
P.Fenwick, A new data structure for cumulative frequency tables, Software Practice and Experience Vol 24, 1994
コード
template <typename T>
struct BinaryIndexedTree {
int n;
vector<T> data;
BinaryIndexedTree(int size) {
n = ++size;
data.assign(n, 0);
}
// get sum of [0,k]
T sum(int k) const {
if (k < 0) return 0;
T ret = 0;
for (++k; k > 0; k -= k&(-k)) ret += data[k];
return ret;
}
// getsum of [l,r]
inline T sum(int l, int r) const { return sum(r) - sum(l-1); }
// data[k] += x
void add(int k, T x) {
for (++k; k < n; k += k&(-k)) data[k] += x;
}
平衡2分探索木
扱うデータ数を\(N\)とすると,平衡2分探索木の各操作と時間計算量は以下.
- 値(大小関係が定義されている必要がある)の挿入: \(O(\log N)\)
- 値の削除: \(O(\log N)\)
- 値の検索/取得: \(O(\log N)\)
データを2分木のノードとして持つことで上記クエリを高速に求める.値の挿入,削除を繰り返す中で,2分木に偏りが出ないように調整することで各クエリの計算量を\(O(\log N)\)に抑えるところから,平衡2分探索木という名前になっている.
平衡2分探索木の実装は多くある.有名な例を下にいくつか挙げる.
- 赤黒木 : C++の
setクラスの内部で使われており,OSの実装におけるタスクスケジューラにも使われていたりする.おそらく最も有名な平衡2分探索木. - AVL木 : こちらも非常に有名な平衡2分探索木.後日加筆.
- Splay木 : Splayという特殊な操作により各種操作の償却計算量を\(O(\log N)\)に抑える(詳しくは該当の章を参照して欲しい).実装が上と比較すると簡単であるため,自実装する必要がある場合はこれがおすすめ.
- 2-3木 : "2分"ではないが,目的は同じ.後日加筆.
- Treap : 後日加筆.
- RBST : 後日加筆.
splay木
splay木は平衡2分探索木の1つである.splay木の各操作と時間計算量は以下.
- 値(大小関係が定義されている必要がある)の挿入: 償却計算量\(O(\log N)\)
- 値の削除: 償却計算量\(O(\log N)\)
- 値の検索/取得: 償却計算量\(O(\log N)\)
償却計算量についてはこの章の後半で説明する.
平衡2分探索木
まず,splay木固有の話ではなく,平衡2分探索木の基本的な説明をする.
平衡2分探索木は,追加された値を各ノードとした2分木を形成する.また,形成された根付き木の,任意のノードについて以下の条件が成り立つようにする.
- 左の子を根とする部分木に含まれる値は全て親より小さい
- 右の子を根とする部分木に含まれる値は全ては親より大きい
平衡2分探索木で,扱う値に大小関係が定義されている必要がある理由は,このように大小関係に基づいて内部の木を形成するからである.では,例えば,値10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150が追加された場合,平衡2分探索木はどのようになるだろうか.
実は,形成される木は複数あり得る.例えば,左下のように偏りがない綺麗な2分木になることもあれば,右下のような木もちゃんと条件を満たしている.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
80((80)) --- 40((40))
80 --- 120((120))
40 --- 20((20))
40 --- 60((60))
120 --- 100((100))
120 --- 140((140))
20 --- 10((10))
20 --- 30((30))
60 --- 50((50))
60 --- 70((70))
100 --- 90((90))
100 --- 110((110))
140 --- 130((130))
140 --- 150((150))
14000((140)) --- 12000((120))
14000 --- 15000((150))
12000 --- 10000((100))
12000 --- 13000((130))
10000 --- 8000((80))
10000 --- 11000((110))
8000 --- 2000((20))
8000 --- 9000((90))
2000 --- 1000((10))
2000 --- 6000((60))
6000 --- 4000((40))
6000 --- 7000((70))
4000 --- 3000((30))
4000 --- 5000((50))
ページが大きくなるので描かないが,もちろん,最も小さい値から,昇順に右の子に次の値が来るような1本道の木も条件を満たしている.では,このように大小関係に基づいて木を形成すると何が嬉しいかというと,値を検索する際,根ノードから始めて,今見ているノードより探索しているノードが大きいか小さいかで左の子と右の子に降りるかを選択して降りるというのを続けるだけで必ず目的のノードにたどり着くことができるということである.
では,ここで木の形について触れる.偏った木と,偏りがない木と,どちらが嬉しいだろうか.偏りがあるということは,その分,深さが深いノードが存在するということ.探索するノードの深さが深いほど,探索する時間は増えてしまう.よって,偏りがない木ほどより嬉しい.そのため,平衡2分探索木には,形成する2分木をなるべく平衡に保つという機能があるのである.より平衡になると,木の高さが,扱っているデータ数を\(N\)として\(O(\log N)\)になるため,各種操作の計算量が全て\(O(\log N)\)になるというわけだ.
ここでもう1つ触れておきたいのは,平衡2分探索木におけるlower_bound,およびupper_boundという操作について.lower_boundは,指定した値以上の最小の値を探索するというもので,upper_boundは,指定した値より大きい最小の値を探索するというもの.これらの操作の実装は,2分探索木で共通していて,AVL木であってもsplay木であってもその他であっても基本的には同じである.それぞれ,下のようなコードで目的のノードを探索することができる.
Node* bound(T k, bool lower) {
Node *left = root, *right = nullptr;
while (left) {
if ((lower && !(k > left->k)) || (!lower && (k < left->k))) {
right = left;
left = left->l;
} else left = left->r;
}
return right;
}
// TODO : このコードの説明を追記予定
値の挿入でも検索でも削除でも,内部でlower_boundを実行することで目的のノードを探索するため,これは平衡2分探索木の最も基本的かつ重要な操作と言える.lower_boundの計算量は,
\(O(\)探索しているノードが存在する深さ\()\)である.平衡2分探索木の全ての操作の計算量はlower_boundの計算量になると考えてよい.
splay木
splay木では,値の検索,削除など全ての操作の中でsplayという特殊な操作を行う.上で,平衡2分探索木の各操作は内部で全てlower_boundを行うと述べた.splay操作は,lower_boundの計算量を\(O(\log N)\)に保証するための操作であると考えるとわかりやすい.splay木では,全ての操作の計算量はsplay操作の計算量となる.
上で,lower/upper_boundについては既に説明したので,検索,削除等の細かい実装については説明しない(このページの1番下に載せたコードを参照して欲しい).というわけで,ここからは,splay操作について説明する.
splay操作
splay操作は,簡単に言うと,あるノードを根にするという操作である.splay木では,アクセスしたノードをsplayして根に持っていくということをする.何のためにするかというと,lower_boundの計算量を抑えるためである.まずは,splayをするとなぜ計算量が抑えられるのかということは説明せずに,単にsplay操作とは何かを説明する.
splay操作は,zig,zig-zag,zig-zigの3つの操作によってノードを根まで持っていく操作である.
zig
zigは,splayしたいノードの親が根ノードである時に行われる操作である.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
P((Par)):::p --- S((Spl)):::splay
P --- C(部分木C)
S --- A(部分木A)
S --- B(部分木B)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
上のような木を下のように変形する.変形した後も,平衡2分探索木の大小関係の条件をちゃんと満たしている.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
SS((Spl)):::splay --- AA(部分木A)
SS --- PP((Par)):::p
PP --- BB(部分木B)
PP --- CC(部分木C)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
この例は,splayしたいノードが根ノードの左の子である場合のzigだが,右の子である場合も左右対称の同様の操作になる.
zig-zag
zig-zagは,splayしたいノードと親ノードの関係が,親ノードと親の親ノードの関係と逆の時に行われる操作である.これは実質,splayしたいノードに対してzigを2回行うことと同じである.なのになぜzigと区別してここに示しているかは,後半の計算量解析の時に分かるので今は考えなくてよい.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
G((GPar)):::p --- P((Par)):::p
G --- D(部分木D)
P --- A(部分木A)
P --- S((Spl)):::splay
S --- B(部分木B)
S --- C(部分木C)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
上のような木を下のように変形する.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
SS((Spl)):::splay --- PP((Par)):::p
SS --- GG((GPar)):::p
PP --- AA(部分木A)
PP --- BB(部分木B)
GG --- CC(部分木C)
GG --- DD(部分木D)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
この例は,splayしたいノードは右の子であり親ノードは左の子であるが,逆の,splayしたいノードが左の子で,親ノードが右の子である場合も左右対称の同様の操作になる.
zig-zig
zig-zigは,splayしたいノードと親ノードの関係が,親ノードと親の親ノードの関係と同じ時に行われる操作である.これは実質,親ノードに対してzigを1回行った後にsplayしたいノードにzigを1回行うことと同じである.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
G((GPar)):::p --- P((Par)):::p
G --- D(部分木D)
P --- S((Spl)):::splay
P --- C(部分木C)
S --- A(部分木A)
S --- B(部分木B)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
上のような木を下のように変形する.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
SS((Spl)):::splay --- AA(部分木A)
SS --- PP((Par)):::p
PP --- BB(部分木B)
PP --- GG((GPar)):::p
GG --- CC(部分木C)
GG --- DD(部分木D)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
この例は,splayしたいノードは左の子であり親ノードも左の子であるが,逆の,splayしたいノードが右の子で,親ノードも右の子である場合も左右対称の同様の操作になる.
splay操作は,splayしたいノードとその親ノード,親の親ノードとの関係から,zig,zig-zag,zig-zigの内適切なものを選んで木を変形(一般に木の回転と呼ばれる)することを繰り返して,そのノードを根まで持っていく操作である.
splay操作の計算量と各操作の計算量との関係
話の流れを切らさないために結論から述べると,splay操作の償却計算量は\(O(\log N)\)である.償却計算量についてはこの後に説明するが,簡単に言うと,一連の操作を行なった時,その1回あたりの計算量の平均を取ると\(O(\log N)\)になるということが保証されるということである.もっと噛み砕いて言うと,バランスの取れていない木で深さの深いノードをsplayすると,それはその操作単体で見ると時間がかかっているかもしれない.しかし,連続して何回もsplay操作を行なった時,全体の計算量が,splay操作回数を\(k\)として\(O(k \log N)\)になることを保証できるということ.これが償却計算量の意味である.splay操作の償却計算量がなぜ\(O(\log N)\)になるかはひとまず置いといて,もしそうなるとしたら何が嬉しいのかを考えよう.
冒頭で,splay操作は,lower_boundの計算量を\(O(\log N)\)に保証するための操作であると述べた.lower_boundの計算量は,
\(O(\)探索しているノードが存在する深さ\()\)
であった.ではsplay操作はどうだろうか.zig1回の操作でそのノードが1つ上に上がり,zig-zagやzig-zigのようにzigを2回行う操作でそのノードが2つ上がるため,splay操作の計算量は
\(O(\)splayしたいノードが存在する深さ\()\)
である.splayするノードと,探索したノードが等しければ,これらは当然同じである.つまり,lower_boundでアクセスしたノードをsplayすることで,lower_boundの計算量をsplay操作の計算量で保証することができるのである.
splay操作の償却計算量の導出
※この章はかなり読むのがしんどいと思います.コードだけ欲しい人は,飛ばして最後までスクロールしてください.
償却計算量とは,上でも述べたように,続けて行なった一連の操作の,平均した1回あたりの計算量である.混同しやすいものとして,平均計算量があるが,これは別物である.平均計算量は,操作を独立したものとして考える.あらゆる入力に対してその操作を1回行なった時の計算量の平均が平均計算量である.大きな違いは,平均計算量の場合,最悪の入力がされ続けた場合,1回あたりの操作の計算量の平均がその計算量に収まるかがわからないが,償却計算量の場合はその計算量に収まることを保証できるということ.
償却計算量の導出には,ポテンシャル解析という手法が用いられる.ポテンシャル解析では,操作が行われる前と後の状態をポテンシャル関数というもので評価する.ポテンシャル関数で評価した値は借金みたいなものと考えるとわかりやすい.後の操作の計算量を悪化させるような操作を行った場合は,その操作自体は速かったとしてもその分を考慮して評価すべきである.これがポテンシャル解析の基本的な考え方である.
ポテンシャル\(\Phi\)が満たす必要のある条件は以下.
- 任意の\(i\)について,\(i\)番目の操作を行なった後の状態\(\Phi_i\)について,\(\Phi_i \geq 0\)
- \(\Phi_0 = 0\)
これらの条件を満たすポテンシャル\(\Phi\)を定義したとする.このとき,行なったある操作の実計算量を\(T\)とすると,この操作の償却計算量\(\tilde{T}\)との間に以下の式が成り立つ.
$$\tilde{T} = T + \Delta\Phi$$
よって,例えば操作を\(k\)回行ったとすると,全操作の合計計算量について,以下の式が成り立つ.
$$\sum_{i=1}^k \tilde{T}_i = \sum_{i=1}^k T_i + \sum_{i=1}^k \Delta \Phi_i$$
ここで重要なことは,上の条件より,\(\Delta\Phi \geq 0\)であるため,\(\sum_{i=1}^k \tilde{T}_i\)を上から抑えることができれば,実計算量\(\sum_{i=1}^k T_i\)も同様の計算量で抑えることができるということである.
上で述べた2つの条件を満たすポテンシャル関数はいくらでも定義できる.しかし,このポテンシャル関数を適切なものにしなければ,\(\Delta\Phi\)が大きくなってしまい,解析の意味がなくなってしまう.splay操作の償却解析において用いるポテンシャル関数\(\Phi\)を,以下のように定義する(と上手くいく).
\(s(x)\) = ノード\(x\)を根とする部分木のサイズ(部分木に含まれるノード数)
\(r(x) = \log_2 s(x)\)
\(\Phi(x) = \sum r(x)\)
木に存在する全ノードの\(r(x)\)の合計をポテンシャルとして定義するのは,直感的にも理にかなっている.なぜなら,深さの深いノードが多くある状態(後の操作の計算量が悪くなりそうな状態)では,そのノードを下(部分木)に持つノード数が多いため,\(\Phi(x) = \sum r(x)\)の値が増加する.
ここから,実際にsplay操作の償却計算量\(\tilde{T}_{splay}\)を導いていく.
\(\tilde{T}_{splay}\)を導くために,まず,\(\tilde{T}_{zig}\),\(\tilde{T}_{zig-zag}\),\(\tilde{T}_{zig-zig}\)を導く.なぜなら,splay操作は,複数回のzig-zagもしくはzig-zig操作と,最後の1回のzig操作から成っているからだ.
zigの償却計算量
zigをもう1度振り返ると,以下のような操作である.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
P((Par)):::p --- S((Spl)):::splay
P --- C(部分木C)
S --- A(部分木A)
S --- B(部分木B)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
上のような木を下のように変形する.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
SS((Spl)):::splay --- AA(部分木A)
SS --- PP((Par)):::p
PP --- BB(部分木B)
PP --- CC(部分木C)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
この操作の償却計算量は以下で表せる.
$$\tilde{T}_{zig} = T_{zig} + \Delta\Phi = T_{zig} + (\sum_x r_{new}(x) - \sum_x r_{pre}(x))$$
zigは1回の操作であるため,\(T_{zig} = 1\)である.あとは,\(\sum_x r_{new}(x) - \sum_x r_{pre}(x)\)の部分を求めたい.先ほどの木の変形に注目すると,zigによって\(r(x)\)の値が変化したのは,実はsplayしたいノード(以下\(s\)ノードと呼ぶ)とその親ノード(以下\(p\)ノードと呼ぶ)だけである.よって,式は以下のように変形できる.
$$\tilde{T}_{zig} = 1 + \lbrace(r_{new}(s) + r_{new}(p)) - (r_{pre}(s) + r_{pre}(p))\rbrace$$
ここで,上の木の変形の図から,\(r_{new}(p) - r_{pre}(p)\)は負であることが分かる.よって,以下の式が成り立つ.
$$\tilde{T}_{zig} \leq 1 + r_{new}(s) - r_{pre}(s) \leq 1 + 3r_{new}(s) - 3r_{pre}(s)$$
なぜ一部係数を\(3\)にしたかは後で分かるので,今はこの式が成り立つことさえ確認できればok.
zig-zagの償却計算量
zig-zagをもう1度振り返ると,以下のような操作である.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
G((GPar)):::p --- P((Par)):::p
G --- D(部分木D)
P --- A(部分木A)
P --- S((Spl)):::splay
S --- B(部分木B)
S --- C(部分木C)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
上のような木を下のように変形する.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
SS((Spl)):::splay --- PP((Par)):::p
SS --- GG((GPar)):::p
PP --- AA(部分木A)
PP --- BB(部分木B)
GG --- CC(部分木C)
GG --- DD(部分木D)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
zigの時と同様に木の変形に注目すると,\(r(x)\)の値が変化したのは\(s\)ノードと\(p\)ノードとその親のノード(以下\(g\)ノードと呼ぶ)だけである.よって,以下の式が成り立つ.
$$\tilde{T}_{zig-zag} = T_{zig-zag} + \Delta\Phi = 2 + r_{new}(s) - r_{pre}(s) + r_{new}(p) - r_{pre}(p) + r_{new}(g) - r_{pre}(g)$$
ここで,上の木の変形の図から,\(r_{pre}(g) = r_{new}(s)\)であること,\(r_{pre}(p)>r_{pre}(s)\)であることから,下のように変形できる. $$\tilde{T}_{zig-zag} \leq 2 - 2r_{pre}(s) + r_{new}(p) + r_{new}(g)$$
ここで,\(r(x)\)は\(\log s(x)\)であることを思い出すと,式は以下のように変形される.
$$\tilde{T}_{zig-zag} \leq \log \frac{s_{new}(p) \times s_{new}(g)}{s_{new}(s) \times s_{new}(s)} + 2 + 2r_{new}(s) - 2r_{pre}(s)$$
ここで,以下の式\((*)\)を示す.
$$\log \frac{s_{new}(p) \times s_{new}(g)}{s_{new}(s) \times s_{new}(s)} \leq -2 \qquad (*)$$
この式を変形して,
$$\frac{s_{new}(p)}{s_{new}(s)} \times \frac{s_{new}(g)}{s_{new}(s)} \leq \frac{1}{4}$$
が得られる.ここで,zig-zagで木を変形した後の図から,
$$\frac{s_{new}(p)}{s_{new}(s)} + \frac{s_{new}(g)}{s_{new}(s)} \leq 1$$
であることが分かる.和の最大値が定められている時,積の最大値はそれら2つの値が等しく,和の最大値\(/2\)である時である(この証明は簡単なので省略する).よって,
$$\frac{s_{new}(p)}{s_{new}(s)} \times \frac{s_{new}(g)}{s_{new}(s)} \leq \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$$
が証明され,式\((*)\)が示された.ここで,元の式に戻ると,式\((*)\)を使って,以下のように変形できることが分かる.
$$\tilde{T}_{zig-zag} \leq \log \frac{s_{new}(p) \times s_{new}(g)}{s_{new}(s) \times s_{new}(s)} + 2 + 2r_{new}(s) - 2r_{pre}(s) \leq 2r_{new}(s) - 2r_{pre}(s)$$
従って,以下の式が示された.
$$\tilde{T}_{zig-zag} \leq 3r_{new}(s) - 3r_{pre}(s)$$
こちらも,なぜ一部の係数を\(3\)にしたかは後で分かるので,この式が成り立つことさえ確認できればok.
zig-zigの償却計算量
zig-zigをもう1度振り返ると,以下のような操作である.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
G((GPar)):::p --- P((Par)):::p
G --- D(部分木D)
P --- S((Spl)):::splay
P --- C(部分木C)
S --- A(部分木A)
S --- B(部分木B)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
上のような木を下のように変形する.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
SS((Spl)):::splay --- AA(部分木A)
SS --- PP((Par)):::p
PP --- BB(部分木B)
PP --- GG((GPar)):::p
GG --- CC(部分木C)
GG --- DD(部分木D)
classDef p stroke-width:4px,stroke:green;
classDef splay stroke-width:4px,stroke:slateblue;
こちらも同様に木の変形に注目すると,\(r(x)\)の値が変化したのは\(s\)ノードと\(p\)ノードと\(g\)ノードだけである.よって,以下の式が成り立つ.
$$\tilde{T}_{zig-zig} = 2 + r_{new}(s) - r_{pre}(s) + r_{new}(p) - r_{pre}(p) + r_{new}(g) - r_{pre}(g)$$
ここで,上の木の図から,\(r_{pre}(p) < r_{pre}(s)\)であること,\(r_{new}(p) > r_{new}(s)\)であること,\(r_{pre}(g) = r_{new}(s)\)であることから,以下のように変形できる.
$$\tilde{T}_{zig-zig} \leq 2 - 2r_{pre}(s) + r_{new}(s) + r_{new}(g)$$
ここで,\(r(x)\)は\(\log s(x)\)であることを思い出すと,式は以下のように変形される.
$$\tilde{T}_{zig-zig} \leq \log \frac{s_{pre}(s) \times s_{new}(g)}{s_{new}(s) \times s_{new}(s)} + 2 + 3r_{new}(s) - 3r_{pre}(s)$$
ここで,上の木の図から,これは少し気づきにくいが
$$\frac{s_{pre}(s)}{s_{new}(s)} + \frac{s_{new}(g)}{s_{new}(s)} \leq 1$$
であることが,それぞれのノードが持つ部分木を注意深く見ると分かる.ここで,先ほどの\((*)\)式の時と同じように,
$$\log \frac{s_{pre}(s) \times s_{new}(g)}{s_{new}(s) \times s_{new}(s)} \leq -2$$
が示せるので,
$$\tilde{T}_{zig-zig} \leq 3r_{new}(s) - 3r_{pre}(s)$$
が得られる.
これで,zig,zig-zag,zig-zig全ての償却計算量が導出した.ここで,splay操作は,複数回のzig-zagもしくはzig-zig操作と,最後の1回のzig操作から成っていることを思い出して欲しい.このことから,splay操作の償却計算量\(\tilde{T}_{splay}\)は,以下の式で表される.
$$\tilde{T}_{splay} = \sum (\tilde{T}_{zig-zag}~\rm{or}~\tilde{T}_{zig-zig}) + \tilde{T}_{zig}$$
そして,splay操作でzig-zagまたはzig-zigをした回数を合計\(m-1\)回,また,splay操作の直前の状態を\(0\)番目の状態とすると,今まで求めてきたものを代入して以下の式が得られる.
$$\tilde{T}_{splay} \leq 1 + 3r_{m}(s) - 3r_{m-1}(s) + \sum_{i=1}^{m-1}(3r_i(s) - 3r_{i-1}(s))$$
これは,一見ごちゃごちゃしているように見えるが,\(\sum\)の部分を展開すると,前の\(3r_i(s)\)と次の\(- 3r_i(s)\)が綺麗に打ち消しあって消える.したがって,以下の式を得る.
$$\tilde{T}_{splay} \leq 1 + 3r_m(s) - 3r_0(s)$$
ここで,\(3r_m(s)\)はsplay操作が終わった後の状態であることに注目する.splay操作が終わった後,\(s\)ノードは根であるため,木の全ノード数を\(N\)とすると,以下の式が成り立つ.
$$r_m(s) = \log N$$
また,\(r(x) \geq 0\)であることから,最後に,splay操作の償却計算量\(\tilde{T}_{splay}\)が得られる.
$$\tilde{T}_{splay} \leq 1 + 3 \log N \leq O(\log N)$$
よって,ここからは冗長だが,splay操作を\(k\)回行った時の計算量について以下の関係が成り立つ.
$$\sum_{i=1}^{k} T_{splay} \leq \sum_{i=1}^{k} \tilde{T}_{splay} \leq O(k \log N)$$
従って,splay操作を連続して行なった時の1回あたりの平均の計算量,つまり償却計算量は,\(O(\log N)\)である.
実装におけるその他の注意事項
lower_boundでアクセスしたノードをsplayするのを忘れてはいけない.それをsplayするから\(O(\log N)\)になるのであって,余分な操作と思ってsplayを省略すると,計算量がおかしくなる.lower_bound以外の方法で,\(O(1)\)以外の方法でノードにアクセスする際は,それがlower_boundと同等のアクセス方法かをよく考えること.また,その後のsplay操作も忘れないこと.
以上!
コード
template <class T> struct Node {
Node<T> *l, *r, *p;
T k;
Node(T k_) : l(nullptr), r(nullptr), p(nullptr), k(k_) {}
int state() {
if (p && p->l == this) return -1;
if (p && p->r == this) return 1;
return 0;
}
void rotate() {
Node<T> *par = p;
Node<T> *mid;
if (p->l == this) {
mid = r; r = par;
par->l = mid;
} else {
mid = l; l = par;
par->r = mid;
}
if (mid) mid->p = par;
p = par->p; par->p = this;
if (p && p->l == par) p->l = this;
if (p && p->r == par) p->r = this;
}
void splay() {
while(state()) {
int st = state() * p->state();
if (st == 0) {
rotate();
} else if (st == 1) {
p->rotate();
rotate();
} else {
rotate();
rotate();
}
}
}
};
template <class T> struct SplayTree {
private:
using NC = Node<T>;
NC *root, *min_, *max_;
int sz;
void splay(NC *node) { node->splay(), root = node; }
NC* bound(T k, bool lower) {
NC *valid = nullptr, *left = root, *right = nullptr;
while (left) {
valid = left;
if ((lower && !(k > left->k)) || (!lower && (k < left->k))) {
right = left;
left = left->l;
} else left = left->r;
}
if (!right && valid) splay(valid);
return right;
}
public:
SplayTree() : root(nullptr), min_(nullptr), max_(nullptr), sz(0) {}
int size() { return sz; }
NC *begin() { return min_; }
NC *rbegin() { return max_; }
NC* lower_bound(T k) {
NC *ret = bound(k, true);
if (ret) splay(ret);
return ret;
}
NC* upper_bound(T k) {
NC *ret = bound(k, false);
if (ret) splay(ret);
return ret;
}
NC* entry(T k) {
lower_bound(k);
if (!root || root->k != k) return nullptr;
return root;
}
pair<NC*, bool> insert(T k) {
NC *nn = new NC(k);
if (!root) { // if no nodes in tree
min_ = nn, max_ = nn, root = nn;
} else if (min_->k > k) { // if k become min k in tree
min_->l = nn, nn->p = min_, min_ = nn;
splay(nn);
} else if (max_->k < k) { // if k become max k in tree
max_->r = nn, nn->p = max_, max_ = nn;
splay(nn);
} else {
NC *node = bound(k, true); // assert node is not null
if (node->k == k) { // if tree already has k k
splay(node); delete nn; return {root, false};
}
// now node is first node whose k is larger than k
nn->l = node->l; node->l = nn;
nn->p = node; if (nn->l) nn->l->p = nn;
splay(nn);
}
sz++; return {root, true};
}
void erase(NC *node) {
assert(node); splay(node); sz--;
if (!root->l) { // it means this node is min_
// if no nodes remain
if (!root->r) root = nullptr, min_ = nullptr, max_ = nullptr;
else {
root = root->r; root->p = nullptr;
for (min_ = root; min_->l; min_ = min_->l);
splay(min_);
}
} else if (!root->r) {
root = root->l; root->p = nullptr;
for (max_ = root; max_->r; max_ = max_->r);
splay(max_);
} else {
root->l->p = nullptr; // cut left tree
NC *nx_root = root->l; // next root
for (;nx_root->r; nx_root = nx_root->r);
splay(nx_root);
// now nx_root doesn't have right child
nx_root->r = node->r; nx_root->r->p = nx_root;
root->p = nullptr;
}
delete node;
}
bool erase(T k) {
if (!entry(k)) return false;
erase(root);
return true;
}
};
RangeBST
扱う座標数を\(N\)とすると,RangeBSTの各操作と時間計算量は以下.
- 構築: 処理なし
- 指定された1次元座標に値(モノイドを成す集合の要素)の設置: \(O(\log N)\)
- 指定された1次元座標の値の更新: \(O(\log N)\)
- 任意の座標区間の"和"(モノイドにおける2項演算) : \(O(\log N)\)
※このRangeBSTという名前は,筆者が勝手につけたもので,このデータ構造には特別名前はなく,中身はBST,つまり平衡2分探索木である.平衡2分探索木に機能を追加することで能力を拡張する例は多々あり,これはその1つの例である.
セグメント木と同じ?と思った方もいるかもしれないが,実は少し違う.セグメント木は,配列に対する区間クエリに対応したもの,つまり,言い換えると座標に制限(0~配列のサイズ)がある.RangeBSTは,データを,座標の集合としてもつため,座標の値自体に制限がなく,座圧+セグ木で解く必要がある問題も,RangeBSTなら座圧せずに解くことができる(データ構造内部でも座圧操作をしない!!)ため,実装が楽になり,実行速度も速くなることがある.
説明
配列に対する区間クエリではないため,最初にサイズを与えたりはしない.使用するメモリ量は,追加した座標の数に比例して動的に増える(座標に重複がある場合は増えない).
例えば,座標10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150にそれぞれ何かしらの値を設置したとする.このとき,平衡2分探索木でこの集合を持つ形は複数あるが,仮に1番綺麗な形として下のようになったとしよう.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
80((80)) --- 40((40))
80 --- 120((120))
40 --- 20((20))
40 --- 60((60))
120 --- 100((100))
120 --- 140((140))
20 --- 10((10))
20 --- 30((30))
60 --- 50((50))
60 --- 70((70))
100 --- 90((90))
100 --- 110((110))
140 --- 130((130))
140 --- 150((150))
ではここで,座標\(25 \sim 115\)の累積"和"を求めよと言われたら,どこのノードの値の"和"を求めればいいかというと,下の赤い部分である.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
80((80)):::p --- 40((40)):::p
80 --- 120((120))
40 --- 20((20))
40 --- 60((60)):::p
120 --- 100((100)):::p
120 --- 140((140))
20 --- 10((10))
20 --- 30((30)):::p
60 --- 50((50)):::p
60 --- 70((70)):::p
100 --- 90((90)):::p
100 --- 110((110)):::p
140 --- 130((130))
140 --- 150((150))
classDef p stroke-width:4px,stroke:orangered;
もちろんそのままやっていてはノード数分の計算量がかかるが,上の赤く塗られたノードを見ると,平衡2分探索木のおかげである程度まとまった位置に求めたいノードが集まっていることがわかる.
じゃあそれぞれのノードが自分を根とする部分木の"和"を持っていたらどうなるかと考えると,見るノードは下の色がついたノードだけでよくなることがわかる.赤いノードはそのノードの値が必要であることを示しており,青いノードはそのノードを根とする部分木の累積"和"が必要であることを示している.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
80((80)):::v --- 40((40)):::v
80 --- 120((120))
40 --- 20((20))
40 --- 60((60)):::p
120 --- 100((100)):::p
120 --- 140((140))
20 --- 10((10))
20 --- 30((30)):::p
60 --- 50((50))
60 --- 70((70))
100 --- 90((90))
100 --- 110((110))
140 --- 130((130))
140 --- 150((150))
classDef v stroke-width:4px,stroke:orangered;
classDef p stroke-width:4px,stroke:slateblue;
とても少なくなった.実は,この工夫だけで,任意区間の累積"和"を求めるのに必要なノード数が\(O(\log N)\)個に抑えられるのである.その理由を説明する.
これは言葉で説明するより図と疑似コードを見た方がわかりやすい.
よりちゃんとした書き方として,累積"和"を取得したい区間を \([25, 115)\)と書く.\([\)は閉区間を意味し,\()\)は開区間を意味する.まず,\(25\)と\(115\)を木上で2分探索(lower_bound)すると,下の緑のノードにたどり着く.また,この2つのノードのLCAをピンク色で示す.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
80((80)):::lca --- 40((40))
80 --- 120((120)):::lb
40 --- 20((20))
40 --- 60((60))
120 --- 100((100))
120 --- 140((140))
20 --- 10((10))
20 --- 30((30)):::lb
60 --- 50((50))
60 --- 70((70))
100 --- 90((90))
100 --- 110((110))
140 --- 130((130))
140 --- 150((150))
classDef v stroke-width:4px,stroke:orangered;
classDef p stroke-width:4px,stroke:slateblue;
classDef lb stroke-width:4px,stroke:green;
classDef lca stroke-width:4px,stroke:deeppink;
左のノードは,LCAまで上りながら,右の部分木がある場合だけその累積"和"を累積すればよく,右のノードも同様に,LCAにまで上りながら,左の部分木がある場合だけその累積"和"を累積すればよい.わかりづらいと思うので,先ほどの図と重ねてみるとわかりやすい.
%%{init: {"flowchart" : { "curve" : "basis" } } }%%
graph TD
80((80)):::lca --- 40((40)):::v
80 --- 120((120)):::lb
40 --- 20((20))
40 --- 60((60)):::p
120 --- 100((100)):::p
120 --- 140((140))
20 --- 10((10))
20 --- 30((30)):::lb
60 --- 50((50))
60 --- 70((70))
100 --- 90((90))
100 --- 110((110))
140 --- 130((130))
140 --- 150((150))
classDef v stroke-width:4px,stroke:orangered;
classDef p stroke-width:4px,stroke:slateblue;
classDef lb stroke-width:4px,stroke:green;
classDef lca stroke-width:4px,stroke:deeppink;
疑似コードを示すとこのようになる.
fn prod(xl: i64, xr: i64) -> S {
let l: *Node = lower_bound(xl);
let r: *Node = lower_bound(xr);
let lca: *Node = get_lca(l, r);
let lprod: S = e();
{ // 左からLCAまで上りながら右側の部分木を累積
for (bool f = true; l != lca;) {
if (f) lprod = op(lprod, l.r.prod_subtree);
f = l.is_left_child();
if (f && l.p != lca) lprod = op(lprod, l.p.v);
l = l->p;
}
}
let rprod: S = e();
{ // 右からLCAまで上りながら左側の部分木を累積
for (bool f = true; r != lca;) {
if (f) rprod = op(r.l.prod_subtree, rprod);
f = r.is_right_child();
if (f && r.p != lca) rprod = op(r.p.v, rprod);
r = r->p;
}
}
return op(op(lprod, lca.v), rprod);
}
よって,区間クエリの処理は,まず木上でlower_boundし,その次に2つのノードからLCAまで上りながら\(O(1)\)の演算を各ステップで行うだけである.したがって,平衡2分探索木の高さが\(\log N\)であることから,計算量は\(O(\log N)\)となる.
最後に,更新クエリや挿入クエリについて説明する.挿入/更新を\(O(\log N)\)で行えることは平衡2分探索木の章を確認して欲しい.挿入/更新後,ノードの累積"和"の値に影響が出るのは該当ノードの祖先ノード高々\(O(\log N)\)個であるため,それらの値を更新していけばよい.計算量は\(O(\log N) + O(\log N) = O(\log N)\)となる.
実装におけるその他の注意事項
モノイドを扱っているため,例のごとく演算の向きを間違えないようにする.
以上!
コード
平衡2分探索木にSplay木を用いた実装.
template <class S, S (*op)(S, S), S (*e)()> struct Node {
Node<S, op, e> *l, *r, *p;
i64 pt;
S v, prod_st;
explicit Node(i64 pt_, S v_)
: l(nullptr), r(nullptr), p(nullptr), pt(pt_), v(v_), prod_st(v_) {}
int state() {
if (p && p->l == this) return -1;
if (p && p->r == this) return 1;
return 0;
}
S get_lprod() {
if (!l) return e();
return l->prod_st;
}
S get_rprod() {
if (!r) return e();
return r->prod_st;
}
void update() {
prod_st = op(op(get_lprod(), v), get_rprod());
}
void rotate() {
Node<S, op, e> *par = p;
Node<S, op, e> *mid;
if (p->l == this) {
mid = r; r = par;
par->l = mid;
} else {
mid = l; l = par;
par->r = mid;
}
if (mid) mid->p = par;
p = par->p; par->p = this;
if (p && p->l == par) p->l = this;
if (p && p->r == par) p->r = this;
par->update(); update();
}
void splay() {
while(state()) {
int st = state() * p->state();
if (st == 0) {
rotate();
} else if (st == 1) {
p->rotate();
rotate();
} else {
rotate();
rotate();
}
}
}
};
template <class S, S (*op)(S, S), S (*e)()> struct RangeBST {
private:
using NC = Node<S, op, e>;
NC *root, *min_, *max_;
void splay(NC *node) { node->splay(), root = node; }
NC* bound(i64 x, bool lower) {
NC *valid = nullptr, *left = root, *right = nullptr;
while (left) {
valid = left;
if ((lower && !(x > left->pt)) || (!lower && (x < left->pt))) {
right = left;
left = left->l;
} else left = left->r;
}
if (!right && valid) splay(valid);
return right;
}
void set(i64 x, S val, bool add) {
NC *nn = new NC(x, val);
// if no nodes in tree
if (!root) {
min_ = nn, max_ = nn, root = nn; return;
} if (min_->pt > x) { // if x become min key in tree
min_->l = nn, nn->p = min_, min_ = nn;
splay(nn); return;
} if (max_->pt < x) { // if x become max key in tree
max_->r = nn, nn->p = max_, max_ = nn;
splay(nn); return;
}
NC *node = bound(x, true); // assert node is not null
if (node->pt == x) { // if tree already has key x
if (add) node->v = op(node->v, val);
else node->v = val;
node->update(); splay(node); delete nn; return;
}
// now node is first node whose key is larger than x
nn->l = node->l; node->l = nn;
nn->p = node; if (nn->l) nn->l->p = nn;
nn->update(); splay(nn);
}
public:
RangeBST() : root(nullptr), min_(nullptr), max_(nullptr) {}
NC* lower_bound(i64 x) {
NC *ret = bound(x, true);
if (ret) splay(ret);
return ret;
}
NC* upper_bound(i64 x) {
NC *ret = bound(x, false);
if (ret) splay(ret);
return ret;
}
S get(i64 x) {
NC *ret = lower_bound(x);
if (!ret || ret->pt != x) return e();
return ret->v;
}
void set(i64 x, S val) { set(x, val, false); }
void add(i64 x, S val) { set(x, val, true); }
S prod(i64 xl, i64 xr) {
assert(xl <= xr);
if (!root || xl > max_->pt || xr <= min_->pt) return e();
if (xl <= min_->pt && xr > max_->pt) return root->prod_st;
if (xl <= min_->pt) return lower_bound(xr)->get_lprod();
lower_bound(xl); // now xl is root
if (xr > max_->pt) return op(root->v, root->get_rprod());
NC *right = bound(xr, true);
NC *tmp = right;
S ret = e();
for (bool f = true; tmp != root;) {
if (f) ret = op(tmp->get_lprod(), ret);
f = tmp->state() == 1;
if (f) ret = op(tmp->p->v, ret);
tmp = tmp->p;
}
if (right) splay(right);
return ret;
}
};
2次元imos法
imos法は,高次元に拡張することができる.ここでは,2次元imos法を説明する.2次元配列の横の長さを\(W\),縦の長さを\(H\)とする.
- 矩形範囲更新: \(O(1)\)
- 2次元配列上の各要素の値の取得\(O(HW)\)
2次元配列の各要素は可換群を成す集合の要素である必要がある.
説明
考え方は1次元のimos法と同じである.2次元imos法では,\((l_x, l_y)\)を左上の座標,\((r_x, r_y)\)を右下とするような矩形(\((l_x, l_y)\)は矩形内,\((r_x, r_y)\)は矩形外の座標)に値\(x\)を作用させる場合,\(l_x, l_y\)に\(x\)を,\(r_x, l_y\)に\(x^{-1}\)を,\(l_x, r_y\)に\(x^{-1}\)を,\(r_x, r_y\)に\(x\)を作用させる.実際の値を得るには,各行ごとに左から累積値を取った後に,各列ごとに上から累積値を取れば良い.
コード
template <class S, S (*op)(S, S), S (*e)(), S (*inv)(S)> struct Imos2D {
private:
vector<vector<S>> v;
public:
Imos2D(int h, int w) { v.assign(h+1, vector<S>(w+1, e())); }
void query(int lx, int ly, int rx, int ry, S x) { // [(lx, ly), (rx, ry))
v[lx][ly] = op(v[lx][ly], x);
v[rx][ly] = op(v[rx][ly], inv(x));
v[lx][ry] = op(v[lx][ry], inv(x));
v[rx][ry] = op(v[rx][ry], x);
}
vector<vector<S>> get_values() {
for (vector<S> &vv: v) rep (i, 1, vv.size())
vv[i] = op(vv[i-1], vv[i]);
rep (j, v[0].size()) rep (i, 1, v.size())
v[i][j] = op(v[i-1][j], v[i][j]);
return move(v);
}
};
Mo's algorithm
Mo's algorithmとは,長さ\(N\)配列に対して,\(Q\)個の区間クエリを合計で\(O((N + Q)\sqrt{N})\)で処理するアルゴリズムである.Mo's algorithmを適用するには,以下の条件を満たしている必要がある.
- 処理する全クエリを先読みできる(オフラインクエリ).
- 配列の各要素が不変.
- 区間\([l, r)\)の結果から区間\([l+1, r)\),\([l−1, r)\),\([l, r−1)\),\([l, r+1)\)の結果をある程度高速に計算できる.(最終的な計算量に影響する.)
- 区間\([l, m)\)と区間\([m, r)\)をマージして\([l, r)\)を高速に計算することができない.(これができるならセグメント木などを使えば良い.)
要するに,少し複雑な区間クエリに高速に対応するためのアルゴリズムである.
説明
オフラインクエリというのは,クエリを,実際に,与えられた順番で処理する必要がないことを意味する.また,上で述べた条件で,\([l, r)\)に対する区間クエリを求めた後に,\([l+1, r)\),\([l−1, r)\),\([l, r−1)\),\([l, r+1)\)のクエリを高速に求められるというのがあった.これは,区間を左/右に1つ伸び縮みした区間のクエリを高速に求められることを意味する.
Mo's algorithmの基本的なアイディアは,クエリを適切に並び替え,全体での区間の伸び縮みの回数を最小限に抑えられば,全体での計算量を抑えられるということである.
ある区間\([l_1, r_1)\)を求めてからある区間\([l_2, r_2)\)までに行われる伸び縮みの回数は,\(|l_1 - l_2| + |r_1 - r_2|\)である.このことから,\((l_i, r_i)\)を座標としてみることで,任意の2つの区間の間の伸び縮み回数は,2次元座標上でのマンハッタン距離を意味することがわかる.
よって,2次元座標上に設置された全ての点を1回ずつ通る道の中で総移動距離が最短のものを見つけ出したいのだが,これは巡回セールスマン問題とほぼ同じ問題であるため,NP困難な問題である.そこで,全体の計算量がある程度小さくなるように全\((l_i, r_i)\)を通る方法として,この図のような通り方を考える.
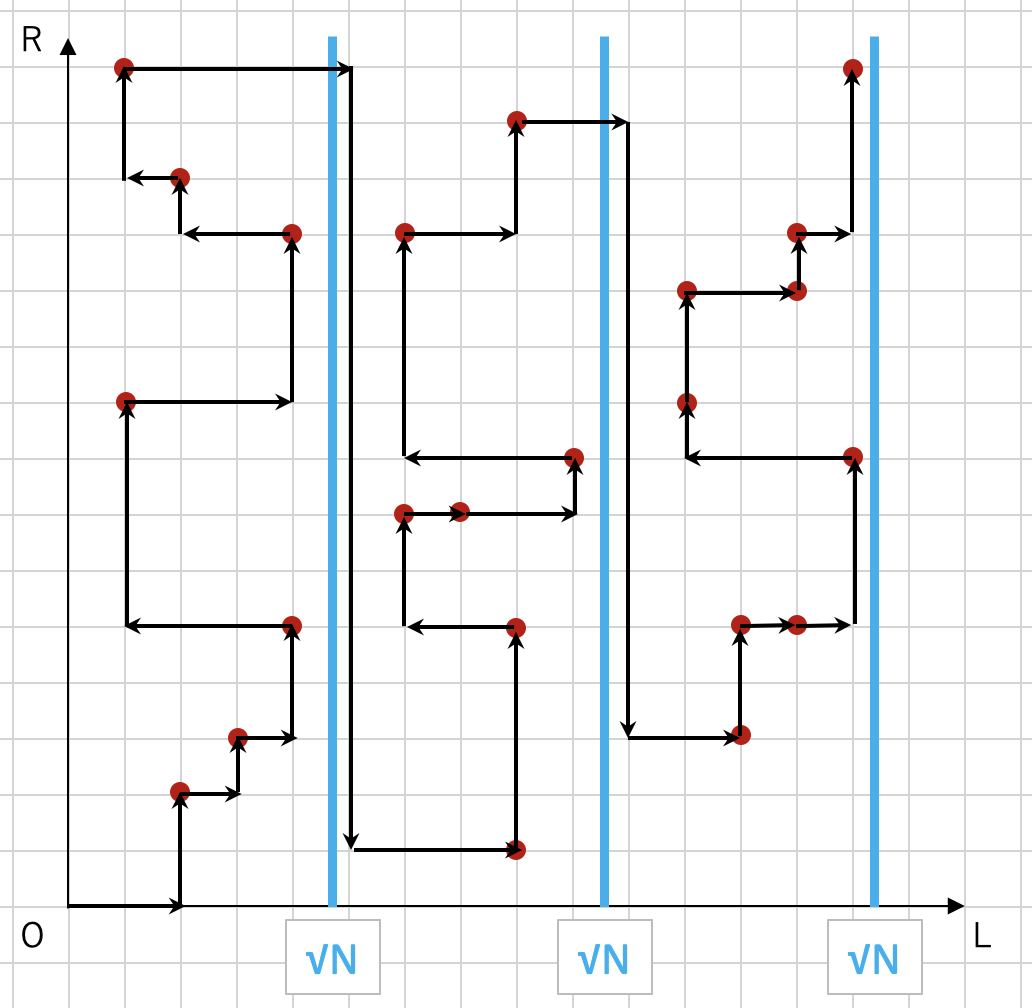
クエリを\(l_i\)について\(\sqrt{N}\)ごとにブロックにわけ,ブロックの昇順に,ブロックごとに\(r_i\)の昇順に点を辿る.
このように辿ることで,ブロックごとに\(r\)の移動は\(O(N)\)でブロック数は\(\sqrt{N}\)なので,全部で\(r\)の移動は\(O(N\sqrt{N})\),また,\(l\)の移動は\(O(\sqrt{N})\)の移動を\(Q\)回繰り返すので,全部で\(l\)の移動は\(O(Q\sqrt{N})\)になる.よって,全体の計算量は\(O((N + Q)\sqrt{N} \times\)区間を\(1\)伸び縮みさせる計算量\()\)である.
このように,クエリについて\(\sqrt{N}\)や\(\sqrt{Q}\)に分割して処理することで全体の計算量を抑える手法は一般に平方分割と呼ばれる.
高速化
Mo's algorithmは,クエリを,上で述べたようにソートするフェーズと,実際に座標を移動しながらクエリを処理するフェーズの2つのフェーズから成る.このうち1つ目のクエリをソートするフェーズについて,ソート方法を工夫することで高速化する方法がいくつかある.
最も有名なのはHilbert曲線に沿って原点から2次元空間を移動する順番(Hilbert Orderと呼ばれる)にクエリを処理する方法である.
Hilbert曲線は,局所性が高く,Hilbert曲線において原点からの距離が近い(Hilbert Orderが近い)ことから,その空間での距離も近いことがわかる.よって,Hilbert Orderでクエリをソートし,その順にクエリを処理することで上で述べた方法よりも全体でかかる計算量が小さくなる.
コード
このコードでは,Hilbert Orderによるソートを用いている.コード中のmaxnの値は,\(N\)以上の(最小の)\(2\)の累乗値にする必要がある.
constexpr int maxn = 1 << ??;
i64 hilbertorder(int x, int y) {
i64 rx, ry, d = 0;
for (i64 s=maxn>>1; s; s>>=1) {
rx = (x & s)>0, ry = (y & s)>0;
d += s * s * ((rx * 3) ^ ry);
if (ry) continue;
if (rx) {
x = maxn-1 - x;
y = maxn-1 - y;
}
swap(x, y);
}
return d;
}
struct Mo {
private:
int q = 0;
vector<int> l, r;
public:
void insert(int l_, int r_) {
q++;
l.emplace_back(l_);
r.emplace_back(r_);
}
// F1~F5: lambda関数
template<typename F1, typename F2, typename F3, typename F4, typename F5>
void execute(F1 &&add_l, F2 &&add_r, F3 &&del_l, F4 &&del_r, F5 &&solve) {
vector<int> qi(q);
iota(all(qi), 0);
vector<i64> eval(q);
rep (q) eval[i] = hilbertorder(l[i], r[i]);
sort(all(qi), [&](int i, int j) {
return eval[i] < eval[j];
});
int nl = 0, nr = 0;
for (int i: qi) {
while (nl > l[i]) add_l(--nl);
while (nr < r[i]) add_r(nr++);
while (nl < l[i]) del_l(nl++);
while (nr > r[i]) del_r(--nr);
solve(i);
}
}
};
ウェーブレット行列
区間スケジューリング問題
区間スケジューリング問題とは以下のような問題である.
\(N\)個のタスクの集合が与えられる.各タスク\(i\)について開始時刻\(s[i]\)と終了時刻\(f[i]\)が定められている.任意の時刻において重複がないようにタスクを選ぶ場合,最大でいくつのタスクを選ぶことができるか.
この問題は,貪欲法により,\(O(N \log N)\)で解くことができる.
説明
終了時刻の早いものから順に重複しない限り選ぶことを繰り返すという貪欲法によってこの問題を解くことができる.
証明
この問題に対する解に含まれる集合を\(OPT\)とし,以降,\(OPT\)に含まれるタスクを終了時刻でソートして\(OPT = \lbrace i_1, i_2, ..., i_o \rbrace\)と表現する.
また,貪欲法により選んだタスクの集合も同様に\(G = \lbrace j_1, j_2, ..., j_g \rbrace\)と表現する.まず,
補題 1
$$\forall k \leq o: f[j_k] \leq f[i_k]$$
を数学的帰納法により示す.
補題1の証明
\(k = 1\)について,貪欲法が最も終了時刻の早いタスクを選択することから,\(f[j_1] \leq f[i_1]\)となることは自明である.
\(k = m\)について,\(f[j_m] \leq f[i_m]\)が成り立つと仮定する.ここで,\(f[j_m] \leq f[i_m] \leq s[i_{m+1}]\)が成り立つ.仮に\(f[i_{m+1}] < f[j_{m+1}]\)なら,貪欲法で\(i_{m+1}\)が選択されるため,\(f[j_{m+1}] \leq f[i_{m+1}]\)が成り立つ.
したがって,数学的帰納法より,補題1が示された.最後に,
定理
上記貪欲法がこの問題に対する解である.
を背理法により示す.
上記貪欲法で選択したタスクの集合が解でないと仮定する.
\(G\)に最後に追加されたタスク\(j_g\)について,補題1より,
$$f[j_g] \leq f[i_g]$$
が成り立つ.ここで,仮定より\(|G| < |OPT|\)であるが,
$$f[j_g] \leq f[i_g] \leq s[i_{g+1}]$$
となり,これは,貪欲法のアルゴリズムで最後にタスク\(j_g\)を加えた後もタスク\(i_{g+1}\)が残っていることを示しているが,上記貪欲法のアルゴリズムと矛盾する.
よって,背理法より,上記貪欲法で選択したタスクの集合がこの問題の解であることが示された.
コード
int interval_scheduling_problem(vector<pair<i64, i64>> &tasks) {
sort(all(tasks), [](pair<i64, i64> &a, pair<i64, i64> &b) {
return a.second < b.second;
});
int ret = 0;
i64 now = 0;
for (pair<i64, i64> &e: tasks) {
if (e.first > now) {
ret++;
now = e.second;
}
}
return ret;
}
重複あり区間スケジューリング問題
区間スケジューリング問題の一般化として,以下のような問題を考える.
\(N\)個のタスクの集合が与えられる.各タスク\(i\)について開始時刻\(s[i]\)と終了時刻\(f[i]\)が定められている.任意の時刻において重複が\(K\)以下になるようにタスクを選ぶ場合,最大でいくつのタスクを選ぶことができるか.
区間スケジューリング問題は,これの\(K=1\)のケースだが,\(K=1\)ではない場合でも解くことができるように,一般化して考える.
この問題は,貪欲法により,\(O(N \log N)\)で解くことができる.
説明
この問題は,全タスクの集合を\(K\)個の集合に分割し,それぞれの集合ごとに独立に\(K=1\)の区間スケジューリング問題を解くというように言い換えることができる.しかし,分割方法は\(O(K^N)\)通りあり,全探索することはできないので,次のタスクをどの集合に割り当てるかを考えながら\(K\)個の区間スケジューリング問題を同時に解くことを考える.
つまり,\(K\)個の終了時刻を管理しながら,次のタスクをどの集合に割り当てるかを選び,選んだものの貪欲法を進めればよい.しかしここで,そのタスクを選ぶことができる状態にあるものが複数ある場合は,どれに割り当てるのが最適かを考える必要があるが,明らかに,終了時刻が最も遅いものを選ぶのが最適である(証明省略).したがって,\(K\)個の重複を許す区間スケジューリングもまた,貪欲法で解くことが可能である.
計算量は,まず最初に,タスクを終了時刻でソートするのに\(O(N \log N)\)かかる.次に,貪欲法では,\(K\)個の終了時刻の内,次のタスクの開始時刻より小さいものの中で最大のものを選ぶことを\(N\)回繰り返すので,multiset(平衡2分探索木) 等を使って\(O(N \log K)\)かかる.よって,最終的な計算量は\(O(N (\log N + \log K))\)だが,問題文から\(K \leq N\)としてよいので\(O(N \log N)\)となる.
コード
int overlapping_interval_scheduling_problem(vector<pair<i64, i64>> &tasks, int k) {
sort(all(tasks), [](pair<i64, i64> &a, pair<i64, i64> &b) {
return a.second < b.second;
});
multiset<i64> now;
rep (k) now.insert(0);
int ret = 0;
for (pair<i64, i64> &e: tasks) {
auto itr = now.lower_bound(e.first);
if (itr != now.begin()) {
itr--;
ret++;
now.erase(itr);
now.insert(e.second);
}
}
return ret;
}
重み付き区間スケジューリング問題
DP
桁DP
確率DP
期待値DP
bitDP
区間DP
耳DP
オートマトンDP
LCS
LIS
フロー
最大フロー問題
2部グラフの最大マッチング
最小費用流問題
ゲーム系問題
後退解析
Nim
Grundy数
群論
後日加筆するかもしれませんが,下の資料がとてもわかりやすいため,リンクを貼ります.
群の定義から,「逆元の存在」を除いたものをモノイドという.