Binary Indexed Tree(フェニック木)

2項演算(以降便宜上仮に"和"と呼ぶ)を与える．区間クエリを求めたい配列の長さを$n$とすると，**Binary Indexed Tree(BIT)**の各操作と時間計算量は以下．

値(モノイド)の更新: $O(\log N)$
配列の始めから任意のインデックスまでの累積"和": $O(\log N)$

説明

配列に単に値を持った場合，値の更新が$O(1)$でできる代わりに任意のインデックスまでの累積"和"を求めるのには$O(N)$かかる．逆に配列にそのインデックスまでの累積"和"を持つと，累積"和"の取得が$O(1)$でできる代わりに値の更新が$O(N)$かかってしまう．工夫すると，実はどちらのクエリにも高速($O(\log N)$)に答えることができる．

$O(\log N)$でこれらの操作をするために，偏りのない2分木を作り，親のノードにその部分木が持つ葉の"和"を持たせるというのが，セグメント木のアイディアであった．

BITでは，数のビット表現に注目する．BITの基本的なアイディアは，任意の自然数がいくつかの2の累乗の和であるのと同様に，累積"和"はいくつかの「サブ累積"和"」の"和"として表すことができるということである．例えばある数をビットで表した時に2つの位置のビットが立っているということは2つの累積"和"を含んでいるということ．

長さ$16$の配列にいくつか値を設置した例を見てみる．

Index	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
保持する区間	1	1...2	3	1...4	5	5...6	7	1...8	9	9...10	11	9...12	13	13...14	15	1...16
設置した値	2	0	1	1	1	0	4	4	0	1	0	1	2	3	0	0
実際の累積"和"	2	2	3	4	5	5	9	13	13	14	14	15	17	20	20	20
格納する値	2	2	1	4	1	1	4	13	0	1	0	2	2	5	0	20

実際に，BITで累積"和"を求めるにはどうするかというのを説明する．例えば閉区間$[0, 13]$の累積"和"を求めてみる．まず$13$を2進数で表す．

$$13_{(10)} = 1101_{(2)}$$

このインデックスに格納された値を足しては最も右にある$1$を削除してそれを新しいインデックスとするという操作を，インデックス値が$0$になるまで繰り返す．

$$1101_{(2)} → 1100_{(2)} → 1000_{(2)} → 0000_{(2)}$$

この例ではインデックス$1101_{(2)} = 13_{(10)}$の値，インデックス$1100_{(2)} = 12_{(10)}$の値，インデックス$1000_{(2)} = 8_{(10)}$の値を足せばいいことになる．上の表で実際に足してみると，$2 + 2 + 13 = 17$となる．これは，閉区間$[0, 13]$の実際の累積"和"の値と一致している．また，$13, 12, 8$が保持する区間を見てみると，$1...8, 9...12, 13$となっていることからも正しい「サブ累積"和"」を足せていることがわかる．

表だとわかりにくいが，これを木構造として見てみるとわかりやすい．

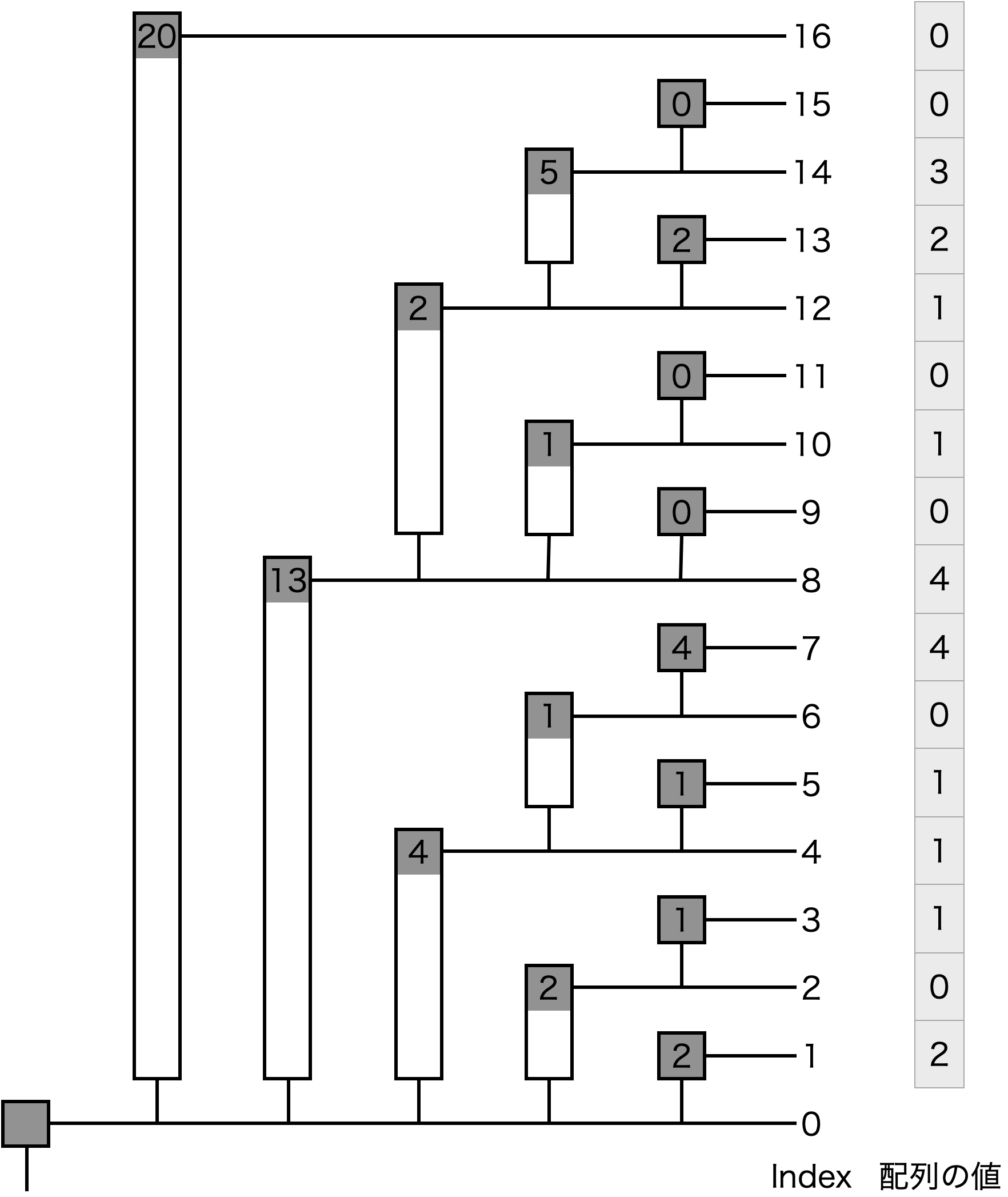
このようにして，ビットが$1$になっているところの個数回の演算で，指定されたインデックスまでの累積"和"を求めることが可能であるため，累積"和"を求めるクエリの計算量は，ビット長から，明らかに$O(\log N)$である．

最後に値の更新だが，あるインデックスを，自身が保持する区間に含めるインデックスの個数も，ビット長から，明らかに$O(\log N)$しかないため，これらのインデックスのみを更新する計算量も，$O(\log N)$である．

template <typename T>
struct BinaryIndexedTree {
  int n;
  vector<T> data;

  BinaryIndexedTree(int size) {
    n = ++size;
    data.assign(n, 0);
  }

  // get sum of [0,k]
  T sum(int k) const {
    if (k < 0) return 0;
    T ret = 0;
    for (++k; k > 0; k -= k&(-k)) ret += data[k];
    return ret;
  }

  // getsum of [l,r]
  inline T sum(int l, int r) const { return sum(r) - sum(l-1); }

  // data[k] += x
  void add(int k, T x) {
    for (++k; k < n; k += k&(-k)) data[k] += x;
  }

アルゴリズムとデータ構造大全

Binary Indexed Tree(フェニック木)

説明

任意区間の累積"和"を求めたい場合

実装

Fenwickさんの論文

コード